giải giúp mk bài này với chiều nay phải có rồi:Khi viết số nguyên dương tăng dần từ 1,2,3,...liên tiếp nhau, ta nhận được dãy số thập phân vô hạn, vd:1234567891011121314... tính tổng n chữ số đầu tiên của dãy số vô hạn trên với nhập từ bàn phím.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


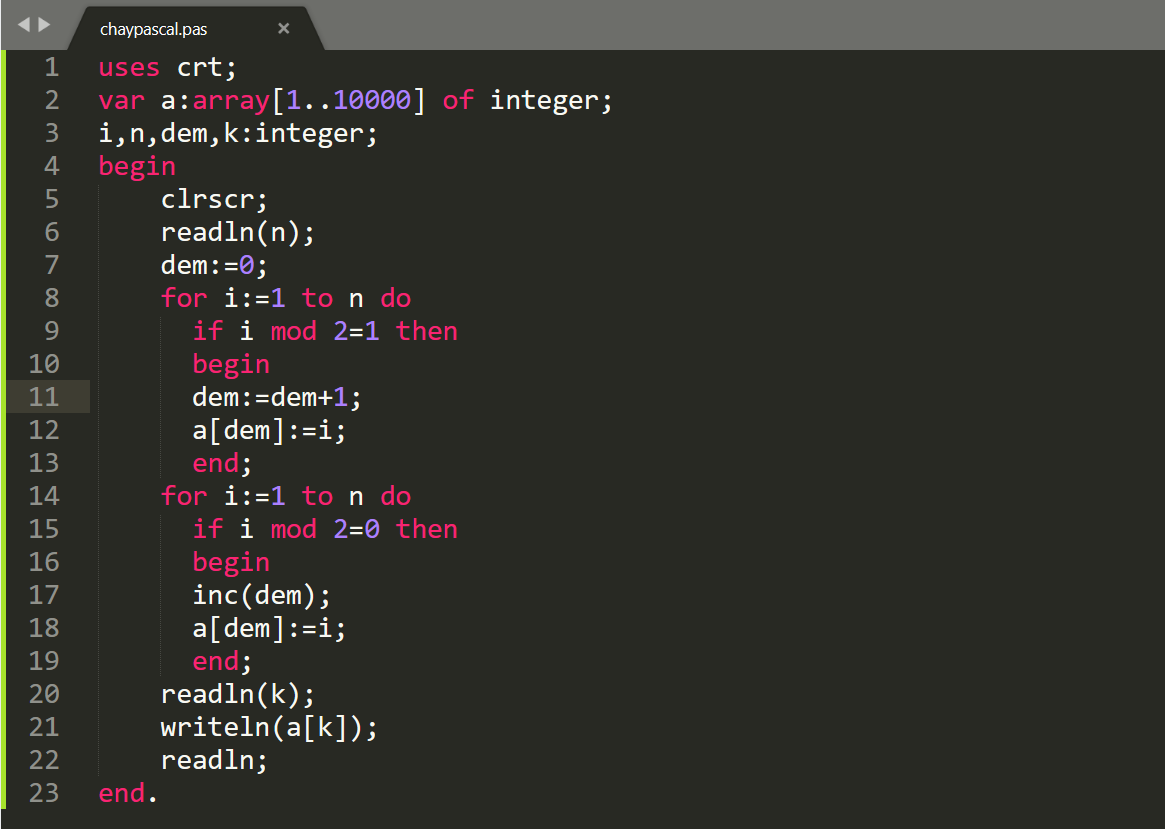
uses crt;
var i,n:integer;
begin
clrscr;
readln(n);
for i:=1 to n do
if i mod 2=1 then write(i:4);
for i:=1 to n do
if i mod 2=0 then write(i:4);
readln;
end.

Số nhà liền kề sẽ cách số nhà liền trước là 2 đơn vị
Số nhà cuối cùng sẽ lớn hơn số nhà đầu tiên là 20.2=40 đơn vị
Gọi a là số nhà đầu tiên, ta có:
a+(a+2)+(a+4)+......(a+40)=900
<=> 20a+(2+4+6+...+40)=900
<=> 20a+2(1+2+3+...+20)=900
<=> 10a+20.21/2 =450 <=> 10a=450-210=240 => a=24
Vậy số nhà đầu tiên là 24
Cách 1:
Dùng công thức tính số số hạng của 1 dãy số cách đều ta tìm được hiệu hai số là:
(SL - SB) : 2 + 1 = 20
SL - SB = 38
Dùng công thức tính tổng của một dãy số cách đều ta tìm được tổng hai số là:
(SL + SB) x 20 : 2 = 900
SL + SB = 90
Nhà đầu tiên được đánh số bé nhất là: (90 - 38) : 2 = 26
Cách 2:
Gọi nhà có số nhỏ nhất là a thì số nhà tiếp theo là a + 2, số nhà lớn nhất là a + 38
Theo bài ra ta có:
a + a + 2 + a + 4 + … + a + 38 = 900
20 x a + 2 + 4 + … + 38 = 900
20 x a + (2 + 38) x 19 : 2 = 900
20 x a + 380 = 900
20 x a = 900 - 380
20 x a = 520
a = 520 : 20
a = 26

Gọi nhà đầu tiên được đánh số nhỏ nhất là \(x\), nhà tiếp theo là \(x+2\), nhà cuối cùng là \(x+38\)
Theo đề bài ra, có:
\(x+x+2+x+4+...+x+38=900\)
\(\Rightarrow20x+2+4+...+38=900\)
\(\Rightarrow20x+\left(2+38\right).19:2=900\)
\(\Rightarrow20x+380=900\)
\(\Rightarrow20x=520\)
\(\Rightarrow x=26\)
Vậy nhà đầu tiên trong dãy phố được đánh là số 26.

Gọi 20 số chẵn liên tiếp lần lượt là a;a+2;...;a+38
Theo đề, ta có:
a+a+2+...+a+38=900
=>20a+380=900
=>a=26
=>Số nhà đầu tiên là 26

a) Cách xác định mỗi số hạng của dãy số:
(1) : Liệt kê
(2) : Nêu cách xác định của mỗi số hạng trong dãy số
(3) : Nêu số hạng tổng quát
(4) : Truy hồi
b) Dãy số có thể cho bằng những cách sau:
- Liệt kê số hạng của dãy số
- Diễn đạt bằng lời cách xác định mỗi số hạng của dãy số
- Cho công thức của số hạng tổng quát
- Truy hồi
Program HOC24;
var m,n,i: byte;
t,d,code: integer;
s,st: string;
begin
write('Nhap N: '); readln(n);
m:=0;
for i:=1 to n do
begin
str(i,s);
st:=st+s;
end;
t:=0;
for i:=1 to n do
begin
val(st[i],d,code);
t:=t+d;
end;
write(t);
readln
end.
program tong;
uses crt;
var n, i, a : integer; x, s : string;
begin
clrscr;
write('nhap n= '); readln(n);
for i:=1 to n do
begin
str(i,s);
x:=x+s;
if length(x)=n then break
end;
{tim n so trong day}
for i:=1 to length(x) do
begin
val(x[i],n);
a:=a+n;
end;
{tinh tong n so trong day}
writeln('tong la ',a);
end.