- 36+x<14+36[x có giá trị lớn nhất].và x+54>54+6[x có giá trị nhỏ nhất]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 6 2019
Đặt \(A=|x+32|+|x-54|\)
\(=|x+32|+|54-x|\ge|x+32+54-x|\)
Hay \(A\ge|86|\)
\(A\ge86\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x+32\right).\left(54-x\right)\ge0\)
\(\Leftrightarrow\hept{\begin{cases}x+32\ge0\\54-x\ge0\end{cases}}\)hoặc \(\hept{\begin{cases}x+32< 0\\54-x< 0\end{cases}}\) ( xin lỗi nha vì OLM ko ghi đc kí hiệu " hoặc" nên mình ghi chữ )
\(\Leftrightarrow\hept{\begin{cases}x\ge-32\\x\le54\end{cases}}\)hoặc \(\hept{\begin{cases}x< 32\\x>54\end{cases}\left(loai\right)}\)
\(\Leftrightarrow-32\le x\le54\)
Vậy MIN A=86 \(\Leftrightarrow-32\le x\le54\)
F
19 tháng 6 2019
Bài giải
Ta có :
\(\left|x+32\right|\ge0\)
\(\left|x-54\right|\ge0\)
\(\Rightarrow\text{ }\left|x +32\right|+\left|x-54\right|\ge0\)
Dấu " = " xảy ra khi \(\hept{\begin{cases}\left|x+32\right|=0\\\left|x-54\right|=0\end{cases}}\) \(\Rightarrow\text{ }\hept{\begin{cases}x=-32\\x=54\end{cases}}\)
Vậy GTNN của \(\left|x+32\right|+\left|x-54\right|=0\)
25 tháng 5 2021
Áp dụng AM-GM có:
\(2a^2+\dfrac{2}{a}+\dfrac{2}{a}\ge3\sqrt[3]{2a^2.\dfrac{2}{a}.\dfrac{2}{a}}=6\)
\(b^2+\dfrac{27}{b}+\dfrac{27}{b}\ge3\sqrt[3]{b^2.\dfrac{27}{b}.\dfrac{27}{b}}=27\)
Cộng vế với vế => \(S\ge33\)
Dấu = xảy ra <=> a=1; b=3
=>T= a+2b=7
CM
30 tháng 6 2017
Chọn C
Tập xác định của hàm số là ℝ .
Ta có: 
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
Khi đó f'(x) = 0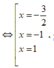 
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
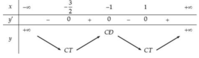
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
CM
8 tháng 8 2019
Hàm số y = a x 2 + b x + c có giá trị nhỏ nhất khi a> 0, khi đó hàm số đạt giá trị nhỏ nhất tại x = − b 2 a
Loại B và C.
* Hàm số y = 4 x 2 – 5 x + 1 đạt giá trị nhỏ nhất tại x = 5 2.4 = 5 8
* Hàm số y = x 2 − 5 2 x + 1 đạt giá trị nhỏ nhất tại x = 5 2 2.1 = 5 4
Đáp án D