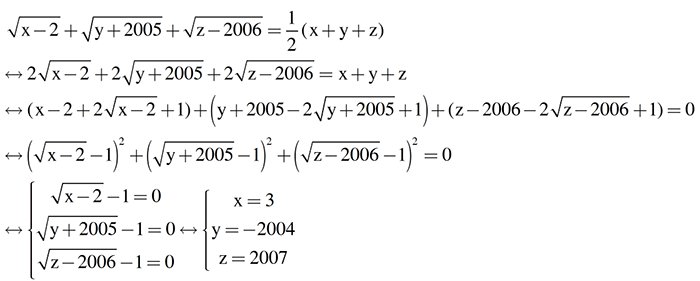Tìm Min P = \(\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
IM
6 tháng 9 2016
Ta có
\(P=\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}\)
\(\Rightarrow P=\left|x+1995\right|+\left|x+1996\right|\)
\(\Rightarrow P=\left|-x-1995\right|+\left|x+1996\right|\)
Ta có \(\begin{cases}\left|-x-1995\right|\ge-x-1995\\\left|1996+x\right|\ge1996+x\end{cases}\)
\(\Rightarrow\left|-x-1995\right|+\left|x+1996\right|\ge-\left(x+1995\right)+\left(x+1996\right)\)
\(\Leftrightarrow P\ge1\)
Dấu " = " xảy ra khi \(\begin{cases}-\left(x+1995\right)\ge0\\x+1996\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\le-1995\\x\ge-1996\end{cases}\)
Vậy MINP=1 khi \(-1996x\le x\le-1995\)
6 tháng 9 2016
Ta có : \(P=\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}=\left|x+1995\right|+\left|x+1996\right|\)
\(=\left|-x-1995\right|+\left|x+1996\right|\ge\left|-x-1995+x+1996\right|=1\)
Dấu "=" xảy ra \(\Leftrightarrow\begin{cases}-x-1995\ge0\\x+1996\ge0\end{cases}\) \(\Leftrightarrow-1996\le x\le-1995\)
Vậy Min P = 1 <=> \(-1996\le x\le-1995\)
TN
7 tháng 9 2016
\(\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}=\left|x+1995\right|+\left|x+1996\right|\)
\(=\left|-x-1995\right|+\left|x-1996\right|\)
Ta chứng minh Bđt \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(\Leftrightarrow\left(\left|a\right|+\left|b\right|\right)^2\ge\left(\left|a+b\right|\right)^2\)
\(\Leftrightarrow a^2+b^2+2\left|ab\right|\ge a^2+b^2+2ab\)
\(\Leftrightarrow\left|ab\right|\ge ab\) luôn đúng
Dấu = khi \(ab\ge0\)
\(\Rightarrow\left|-x-1995\right|+\left|x+1996\right|\ge\left|-x-1995+x+1996\right|=1\)
Dấu = khi \(\left(x+1995\right)\left(x+1996\right)\ge0\)\(\Rightarrow1995\le x\le1996\)
\(\Rightarrow\hept{\begin{cases}1995\le x\le1996\\\left(x+1995\right)\left(x+1996\right)=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1995\\x=-1996\end{cases}}\)
11 tháng 8 2018
Đặt √x = a > 0 thì có
P.2.a(a + 1) - (a - 2)(a - 3) = 0
<=> (2P - 1)x2 + (2P + 5)x - 6 = 0
Để có nghiệm thì:
∆ = (2P + 5)2 - 4.6.(2P - 1) >= 0
Xong rồi đó. Tìm được P >= đó bé
AH
Akai Haruma
Giáo viên
31 tháng 12 2020
a) Đặt $\sqrt{x+1}=a; \sqrt{9-x}=b$ thì bài toán trở thành:
Tìm max, min của $f(a,b)=a+b$ với $a,b\geq 0$ và $a^2+b^2=10$Ta có:
$f^2(a,b)=(a+b)^2=a^2+b^2+2ab=10+2ab\geq 10$ do $ab\geq 0$
$\Rightarrow f(a,b)\geq \sqrt{10}$ hay $f_{\min}=\sqrt{10}$
Mặt khác: $f^2(a,b)=(a+b)^2\leq 2(a^2+b^2)=20$ (theo BĐT AM-GM)
$\Rightarrow f(a,b)\leq \sqrt{20}=2\sqrt{5}$ hay $f_{\max}=2\sqrt{5}$
b)
Đặt $\sqrt{x}=a; \sqrt{2-x}=b$ thì bài toán trở thành:
Tìm max, min của $f(a,b)=a+b+ab$ với $a,b\geq 0$ và $a^2+b^2=2$. Ta có:
$f(a,b)=\sqrt{(a+b)^2}+ab=\sqrt{a^2+b^2+2ab}+ab=\sqrt{2+2ab}+ab\geq \sqrt{2}$ do $ab\geq 0$
Vậy $f_{\min}=\sqrt{2}$
Lại có, theo BĐT AM-GM:
$f(a,b)=\sqrt{2+2ab}+ab\leq \sqrt{2+a^2+b^2}+\frac{a^2+b^2}{2}=\sqrt{2+2}+\frac{2}{2}=3$
Vậy $f_{\max}=3$
AH
Akai Haruma
Giáo viên
31 tháng 12 2020
c) Đặt $\sqrt{8-x^2}=a$ thì bài toán trở thành tìm max, min của:
$f(x,a)=x+a+ax$ với $x,a\geq 0$ và $x^2+a^2=8$. Bài này chuyển về y hệt như phần b.
$f_{\min}=2\sqrt{2}$
$f_{\max}=8$
d) Tương tự:
$f_{\min}=2$ khi $x=\pm 2$
$f_{\max}=2+2\sqrt{2}$ khi $x=0$