1.Mẹ gửi tiết liệm 30 triệu đồng gồm 92 tờ giấy bạc giá 100.000đồng,200.000đồng,500.000đồng trong đó có 4 tờ 100.000đồng.Hỏi có bao nhiêu tờ 200.000đồng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tờ giấy mệnh giá 500 000 đồng là :
3100 000 : 500 000 = 62 ( tờ )
Số tờ giấy mệnh 200000 đồng là :
80 - 62 = 18 ( tờ )
Đ/số : giá 500 000 đồng : 62 tờ
giá 200 000 đồng : 18 tờ
tk mk nha ( nếu đúng )
hihi mơn m.n nhiều nha // cmt sao nha !

Gọi số tờ tiền 2000 đồng là a ; số tờ tiền 5000 đồng là b
Ta có : a + b = 150 (1)
=> 2000 x (a + b) = 2000 x 150
=> 2000 x a + 2000 x b = 300000 (2)
Lại có 2000 x a + 5000 x b = 600000 (3)
Lấy (3) trừ (2) theo vế ta có
2000 x a + 5000 x b - (2000 x a + 2000 x b) = 600000 - 300000
=> 2000 x a + 5000 x b - 2000 x a + 2000 x b = 300000
=> 3000 x b = 300000
=> b = 100
Thay b = 100 vào (1) ta có
a + 100 = 150
=> a = 50
Vậy số tờ tiền 2000 đồng là 50 tờ ; số tờ tiền 5000 đồng là 100 tờ

Cọc thứ nhất có số tờ giấy bạc là:
50000000 : 20000 = 2500 (tờ)
Cọc thứ 2 có số tờ giấy bạc là:
100000000 : 50000000 = 2 (tờ)
Vậy cọc tiền có nhiều tờ giấy bạc hơn cọc thứ nhất.
Hơn số tờ giấy bạc là:
2500 - 2 = 2498 (tờ)
Đáp số:Cọc tiền thứ 2 có nhiều tờ giấy bạc hơn và hơn 2498 tờ
cọc tiền thứ nhất có:50000 : 20000 = 2500 tò
cọc tiền thu hai co : 100000000 : 50000000 = 2 tò
vậy cọc tiền thứ nhất có nhiều tờ giấy bạc hơn và hơn : 2500-2=2598 tò

tờ 5000 = 64000 :5000 = 12 tờ 5000đ
tờ 2000 = 4000:2000= 2 tờ 2000đ

Gọi x là số tờ giấy bạc loại 5 000 đồng người đó có (0 < x < 15 , x ∈ N).
Vì tổng số tờ 2 000 đồng và 5 000 đồng là 15 tờ nên ta có điều kiện x < 15
và số tờ 2 000 đồng người đó có là: 15 – x (tờ)
⇒ Tổng số tiền người đó có là: 5.x + 2.(15 – x) (nghìn đồng).
Theo bài ra, người đó có số tiền không quá 70 nghìn đồng nên ta có bất phương trình:
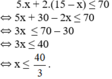
Kết hợp với điều kiện nên x có thể nhận một trong các giá trị {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}