cho đường thẳng AB và CD cắt nhau tại M.các bạn vẽ như thế nào giống đề là được.
CM góc AMD = góc BMC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho đường thẳng AB và CD cắt nhau tại M.các bạn vẽ như thế nào giống đề là được.
CM góc AMD = góc BMC


a/ Ta có AB vuông góc với DC => IC =ID
Tam giác CMD cân tại M và I là trung điểm của DC nên MI vuông góc với DC
Từ hai cái trên ta kết luận M,A,B thẳng hàng
b/ Theo đề bài và câu a ta có
CI = ID
AI = IO
=> Tứ giác OCAD là hình bình hành
ta lại có AO vuông góc với CD
=> Tứ giác OCAD là hình thoi

Có \(\widehat{CMA}+\widehat{CMB}=180^0\) (Hai góc kề bù)
\(\Leftrightarrow5\widehat{CMA}+\widehat{CMA}=180^0\Leftrightarrow\widehat{CMA}=30^0\)
\(\Rightarrow\widehat{BMC}=5.30^0=150^0\)
Có \(\widehat{CMA}+\widehat{AMD}=180^0\)
\(\Leftrightarrow\widehat{AMD}=180^0-30^0=150^0\)
Có \(\widehat{DMB}=\widehat{AMC}=150^0\) (Hai góc đối đỉnh)
Vậy...

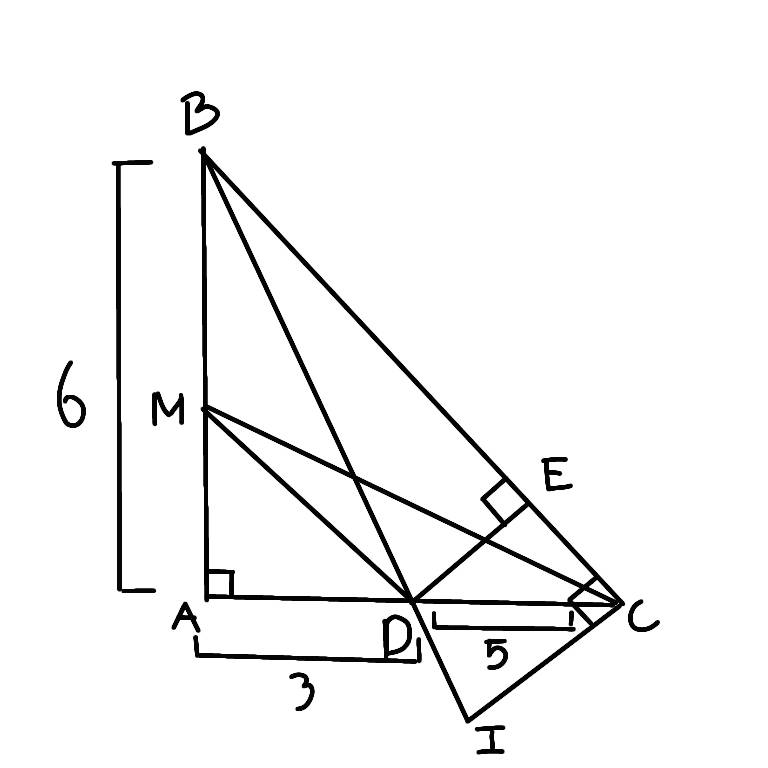 a. Tính BC
a. Tính BC
BC^2 = AC^2 + AB^2
BC^2 = 6^2 + ( AD + DC )^2 = 8^2
BC^2 = 36 + 64 = 100
BC = căng bậc 100 = 10 cm
Tính tỉ số diện tích
Xét tam giác ABC có MD // BC
tam giác AMD ~ tam giác ABC
=>Diện tích tam giác AMD / Diện tích tam giác ABC = (AD/AC)^2=(3/8)^2=9/16 cm2
b.Xét tam giác AMD và tam giác EDC có
Góc MAD = góc CED = 90° (gt)
Góc D chung
=> tam giác AMD ~ tam giác EDC (g.g)
=>MD/AD = DC/EC
=>MD.EC=AD.DC
c. Xét tam giác BCI và tam giác BDE có
Góc BCI = Góc BED = 90°(gt)
Góc B chung
=> Tam giác BCI ~ tam giác BDE(g.g)
=> BC/BI = BD/BE
=> BC.BE = BI.BD(1)
Xét tam giác CBA và tam giác CDE có
Góc CAB = góc CED =90° (gt)
Góc C chung
=> Tam giác CBA ~ tam giác CDE(g.g)
=> CB/CA=CD/CE
=> CB.CE = CA.CD(2)
Từ (1) và (2) ta cộng cho 2 vế
=>BC.BE + CB.CE = BD.BI + CA.CD
=>(BE+CE)BC = BD.BI + CA.CD
=> BC.BC = BD.BI + CA.CD
=> BC^2 = BD.BI + CA.CD
Ta có : góc AMD+góc DMB=180 (Kề bù)
góc BMC + góc DMB=180 (Kề bù)
=> góc AMD +góc DMB=góc BMC+ góc DMB
=>góc AMD=góc BMC