Cho 4 điểm A, C', D', B theo thứ tứ nằm trên cùng một đường thẳng a
Trong cùng 1 nửa mặt phẳng bờ a vẽ các hình vuông ABCD và A'B'C'D'
CMR: AA', BB', CC', DD' đồng quy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
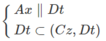
⇒ Ax // (Cz,Dt)
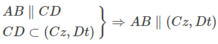
Từ Ax, AB ⊂ (Ax,By) suy ra (Ax, By) // (Cz, Dt)
Tương tự ta có (Ax, Dt) // (By,Cz)
b)
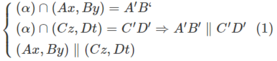
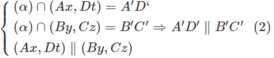
Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.
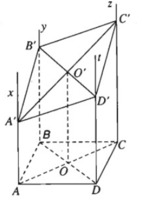
c) Gọi O, O’ lần lượt là tâm các hình bình hành ABCD, A’B’C’D’. Dễ thấy OO’ là đường trung bình của hình thang AA’, suy ra 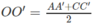
Tương tự ta có:
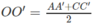


Aa//Bb vì có góc xAa và góc x'Bb là 2 góc ngoài cùng phía bù nhau
Bb//Cc vì có góc xCc= góc x'Bb là 2 góc so le trong
Đây là kiến thức cơ bản mà
Gọi O là giao điểm của AA' và BB'. Ta sẽ chứng minh rằng các đường thẳng CC', DD' cũng đi qua O. Thật vậy:
\(\frac{OB'}{OB}=\frac{OA'}{OA}=\frac{A'B'}{AB}=\frac{B'C'}{BC}\)
Do đó tam giác OB'C' và tam giác OBC đồng dạng (c.g.c)
=> góc B'OC' = góc BOC
từ đó C, O, C' thẳng hàng hay CC' đi qua O
tương tự DDO'