giải và biện luận phương trình này với: m^2x+3x=m(4x+1)+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
1
4 tháng 12 2021
a: Để phương trình có nghiệm duy nhất thì \(\left(m-3\right)\left(m+2\right)\ne0\)
hay \(m\notin\left\{3;-2\right\}\)
Để phương trình có vô số nghiệm thì \(m-3=0\)
hay m=3
Để phương trình vô nghiệm thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+2\right)=0\\m^2-4m+3< >0\end{matrix}\right.\Leftrightarrow m=-2\)
5 tháng 12 2021
a: Để phương trình có nghiệm duy nhất thì \(\left(m-3\right)\left(m+2\right)< >0\)
hay \(m\notin\left\{3;-2\right\}\)
Để phương trình vô nghiệm thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+2\right)=0\\\left(m-3\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-2\)
Để phương trình có vô số nghiệm thì m=3
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2021
1.
\(\Leftrightarrow\left(m^2+4\right)x\ge2-m\)
Do \(m^2+4>0\) ; \(\forall m\)
\(\Rightarrow x\ge\dfrac{2-m}{m^2+4}\)
2.
\(\Leftrightarrow2mx-2x\ge m-1\Leftrightarrow2\left(m-1\right)x\ge m-1\)
- Với \(m>1\Rightarrow m-1>0\)
\(\Rightarrow x\ge\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\ge\dfrac{1}{2}\) \(\Rightarrow D=[\dfrac{1}{2};+\infty)\)
- Với \(m< 1\Rightarrow m-1< 0\Rightarrow x\le\dfrac{m-1}{2\left(m-1\right)}\Leftrightarrow x\le\dfrac{1}{2}\) \(\Rightarrow D=(-\infty;\dfrac{1}{2}]\)
- Với \(m=1\Leftrightarrow0\ge0\Rightarrow D=R\)
Quan sát 3 TH ta thấy không tồn tại m để tập nghiệm của BPT là \([1;+\infty)\)
PT
1
CM
13 tháng 1 2018
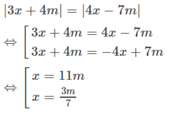
Vậy phương trình đã cho có hai nghiệm x = 11m và x = 3m/7 với mọi giá trị của m.
NX
0
T
1
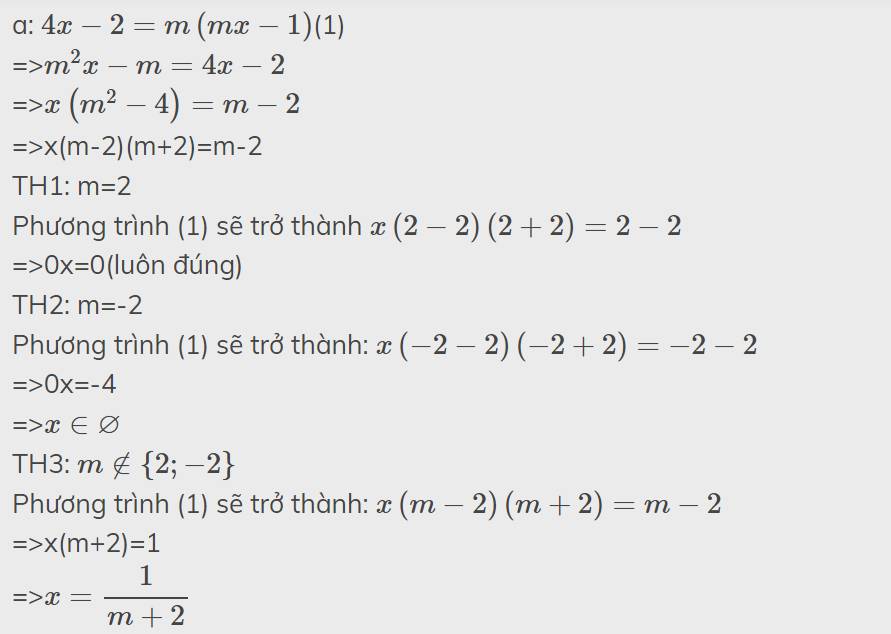
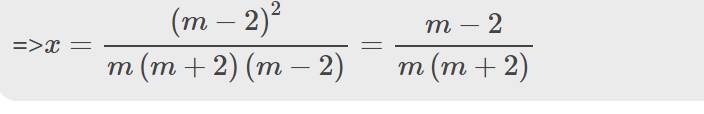
\(m^2x+3x=m\left(4x+1\right)+3\)
\(\Leftrightarrow m^2x+3x=4mx+m+3\)
\(\Leftrightarrow x\left(m^2-4m+3\right)=m+3\)
\(\Leftrightarrow x\left(m-3\right)\left(m-1\right)=m+3\)
+) Nếu \(m\ne1;3\)thì phương trình có nghiệm duy nhất \(x=\frac{m+3}{\left(m-1\right)\left(m-3\right)}\)
+) Nếu m = 1 thì \(pt\Leftrightarrow0x=4\)( vô lí )
\(\Rightarrow\) pt vô nghiệm
+) Nếu m = 3 thì \(pt\Leftrightarrow0x=6\) ( vô lí )
\(\Rightarrow\)phương trình vô nghiệm