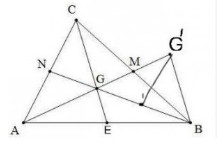
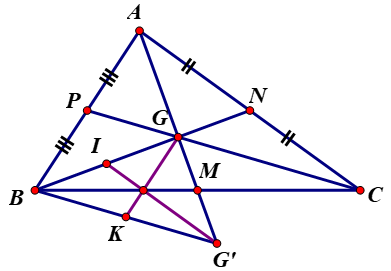
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC

 AM
AM AG ( G là trọng tâm )
AG ( G là trọng tâm )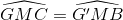
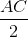
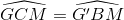 (lại góc sole trong)
(lại góc sole trong)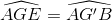 (đồng vị)
(đồng vị)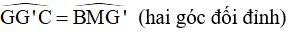
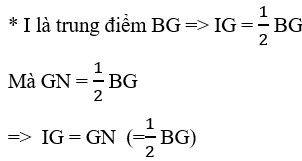
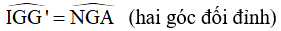
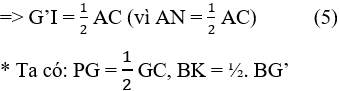

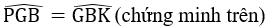
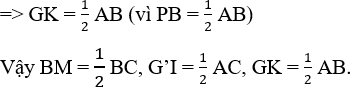
Bài giải
a) Gọi M, N, E lần lượt là trung điểm của AB, BC, CA.
Vậy mỗi cạnh của ΔBGG' bằng 2/3 đường trung tuyến của ΔABC.
b) Gọi I, K lần lượt là trung điểm của BG và BG'.