Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


các bạn giúp mình nhé sáng thứ tư mình nộp bài rồi cảm ơn

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
BD=CE
góc ABD=góc ACE
=>ΔADB=ΔAEC
=>AB=AC
=>ΔABC cân tại A
b: ΔABC cân tại A
mà AD là đường phân giác
nên AD vuông góc BC
Xét ΔABC có
AD,CH là đường cao
AD cắt CH tại D
=>D là trực tâm
=>BD vuông góc AC

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
góc BAE chung
Do đó: ΔABE=ΔACF
=>BE=CF
b:
Sửa đề Chứng minh BE+CF>BH+CH
BE>BH
CF>CH
=>BE+CF>BH+CH

a) Xét \(\Delta\)ABH và \(\Delta\)ACK, có:
góc BAC chung
AB=AC(\(\Delta\)ABC cân) }=> \(\Delta\)ABH và \(\Delta\)ACK(cạnh huyền-góc nhọn)
góc K= góc H(=90 độ)
Vậy \(\Delta\)ABH và \(\Delta\)ACK
b) Vì \(\Delta\)ABH và \(\Delta\)ACK(c/m trên)
=> AK=AH(2 cạnh tg ứng)
Ta có: AB= AK+BK
AC= AH+CH
Mà AB=AC(\(\Delta\)ABC cân)
AK=AH(c/m trên)
=> BK=CK
Vậy BK=CK
c) Xét \(\Delta\)ABC, có:
BH là đường cao thứ nhất
CK là đường cao thứ hai
Mà BH cắt Ck tại I
=> I là trực tâm \(\Delta\)ABC
=> AI là đường cao \(\Delta\)ABC
=> AI vuông góc BC
Vậy AI vuông góc BC
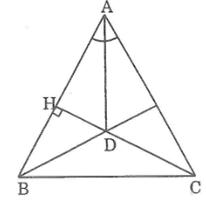
Vì CH là đường cao nên CH vuông BC
\(BC^2=BH^2+CH^2\)(1)
\(AC^2=AH^2+HC^2\)(2)
Lấy (1) - (2) ta được :
\(BC^2-AC^2=BH^2-AH^2\)
mà tam giác ABC cân nên CH là đường cao hay CH là trung tuyến
\(\Rightarrow BC^2-AC^2=0\Rightarrow BC^2=AC^2\)
lại có : \(AC^2=AB^2\Rightarrow BC^2=AB^2=AB.AB=2BH.AB\)( đpcm )
https://www.googleadservices.com/pagead/aclk?sa=L&ai=C1xTO4p68YNz8KZW9qAHPy5LIDMmr6qNg0NOfg5kLwI23ARABINzsuC5gwQWgAZ7U484DyAEBqQINxZei7dzHPagDAcgDwwSqBMsBT9BTpRx9neIyrGO0O1963KuNmKBbxmGUtm-UAFO5AJXWfGhNypiODjI2tMBBsAxtTOKP603Lj3je5QQRx3ovhk8kcnnZ93EdoUFKtIfQ7jNaTP1DRpyH3y7auZXCUyvspX9qBZEFNAcV6T0_zEqR9ahsF-pKVxzj0G4oSE7mhCvi1sG4B097ERVJq_aNPyK_D7SmVwoVrcjkAfcWeX7qSdiA0lC5ml0043ZOXX-lVQaHdEX1us_fzL7ZFFc6436j-L8Q9e9-AVNaNvzABKml1oj1AqAGUYAHyqucMagHipyxAqgH1ckbqAfw2RuoB_LZG6gHjs4bqAeT2BuoB7oGqAfulrECqAemvhuoB-zVG6gH89EbqAfs1RuoB5bYG9gHAdIIBwiAYRABGB-xCelDaA8avH1pgAoBmAsByAsBuAwB2BMN0BUBmBYBgBcB&ae=1&num=1&cid=CAASEuRosVrTt0fMF44rjoYpSKVXWQ&sig=AOD64_3I3-_NQIpH8DjLwEZVT3ytqgp_Iw&client=ca-pub-2208223212947843&nb=1&adurl=https://hoidap247.com/%3Fgclid%3DEAIaIQobChMI3PWZ--GC8QIVlR4qCh3PpQTJEAEYASAAEgJrHfD_BwE