Cho tam giác ABC có góc ABC = góc ACB = 36o . Trên tia phân giác của góc ABC lấy điểm N sao cho góc BCN = 12o . So sánh độ dài CN và CA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2016
Ta có hình vẽ
a) Xét tam giác ACE và tam giác DCE, ta có:
AC=DC( giả thiết)
Góc ACE=Góc ECD (vì tia x là tia phân giác của góc C)
CE là cạnh chung
Do đó: tam giác ACE=tam giác DCE (c-g-c)
b) Có vẻ như đề của bạn thiếu nên mình giúp bạn câu a) thôi nhé! ^^
R
31 tháng 1 2022
a) Xét \(\Delta ACE\) và \(\Delta DCE\) có :
- CE chung
\(CD=CA\)
\(\Rightarrow\Delta ACE=\Delta DCE\)
\(\Rightarrow EA=ED\)
b) \(\Delta ACE=\Delta DCE\Rightarrow EDC=EAC=90^0\Rightarrow DEB+EBD=90^0\)
Mà \(BCA+EBD=90^o\Rightarrow BED=BCA\)
H
31 tháng 1 2022
Tự vẽ hình
a, xét tam giác ACE và tam giác DCE có
CD = CA ( gt)
góc DCE = góc ACE ( CE là tia phân giác)
CE chung
=>tam giác ACE = tam giác DCE ( c-g-c)
=> EA = ED, góc CDE = góc CAE (=90 độ)
b, Xét tam giác BDE vuông tại E ( vì góc CDE = 90 độ kề bù vs góc EDB nên góc EDB cx = 90 độ)
Góc DBE + góc DEB = 90 độ ( hai góc phụ nhau) (1)
Xét tam giác ABC vuông tại A ( gt)
=> góc ABC + góc ACB 90 độ ( hai góc phụ nhau) ( 2)
Từ (1) và (2) => góc BED = góc ACB ( cùng phụ vs góc EBD)
4 tháng 4 2018
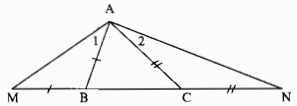
Trong ∆ABC có AB < AC
⇒ góc ABC= góc ACB (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
⇒ góc ∆ABM cân tại B
⇒ góc M = góc A1(tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
góc ABC= góc M+ góc A1
Suy ra: góc M=12 góc ABC (2)
Ta có: AC = CN (gt)
⇒ ∆CAN cân tại C⇒ góc N= góc A2 (tính chất tam giác cân)
Trong ∆CAN ta có góc ACB là góc ngoài tại đỉnh C.
⇒góc ACB= góc N+ góc A2
Suy ra: góc N=12 góc ACB (3)
Từ (1), (2) và (3) suy ra: góc M > góc N
b) Trong ∆AMN ta có: góc M> góc N
Trên tia BA lấy M sao cho BM=BC.
Chứng minh
ΔBMN=ΔBCN ⇒ NM=NC;ˆMNC=60o
⇒ΔMNCΔBMN=ΔBCN
⇒NM=NC;MNC^=60o
⇒ΔMNC đều.
Xét ΔMAC ΔMAC cân tại C (Cái này tính góc là chứng minh được)
⇒MC=AC⇒AC=CN⇒MC=AC⇒AC=CN
tahm khảo mk chả bít có đúng ko