Cho hình bình hành ABCD. Vẽ AH vuông góc với CD, AK vuông góc với BC. CMR: Tam giác KAH đồng dạng với tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 5 2017
* Trường hợp góc B nhọn:
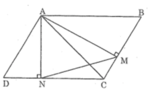
Xét △ AMB và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
B = D (t/chất hình bình hành) ⇒ △ AMB đồng dạng △ AND (g.g)
Suy ra: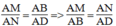 
Mà AD = BC (t/chất hình hình hành)
Suy ra: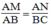 
Lại có: AB // CD (gt)
AN ⊥ CD (gt)
Suy ra: AN ⊥ AB hay ∠ (NAB) = 90 0
suy ra: ∠ NAM + ∠ MAB = 90 0 (1)
Trong tam giác vuông AMB ta có ∠ ABM = 90 0
Suy ra: ∠ (MAB) + ∠ B = 90 0 (2)
Từ (1) và (2) suy ra: ∠ NAM = ∠ B
Xét △ ABC và △ MAN ta có:
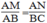(chứng minh trên)
∠ (NAM) = ∠ B (chứng minh trên)
Vậy △ ABC đồng dạng △ MAN (c.g.c)
* Trường hợp góc B tù:
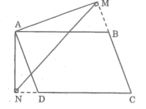
Xét △ MAN và △ AND, ta có:
∠ (AMB) = ∠ (AND) = 90 0
∠ (ABM) = ∠ (ADN) (vì cùng bằng C)
⇒ △ AMB đông dạng △ AND (g.g)
Suy ra: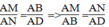
Mà AD = BC (t/chẩt hình bình hành)
Suy ra: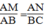 
Vì AB //CD nên ∠ (ABC) + ∠ C = 180 0 (3)
Tứ giác AMCN có ∠ (AMC) = ∠ (AND) = 90 0
Suy ra: ∠ (MAN) + ∠ C = 180 0 (4)
Từ (3) và (4) suy ra: (MAN) = (ABC)
Xét △ AMN và △ ABC, ta có:
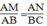(chứng minh trên)
∠ (MAN) = ∠ (ABC) (chứng minh trên)
Vậy △ MAN đồng dạng △ ABC (c.g.c)
