Áp dụng hệ thức bất định Heisenberg để tính độ bất định về vị trí cho trường hợp electron chuyển động trong nguyên tử với giả thiết Δvx = 106 m/s. Cho biết me = 9,1.10-31 kg; h = 6,625.10-34 J.s.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2014
Mà \(\Delta\)px.\(\Delta\)x=m.\(\Delta\)Vx.\(\Delta\)x =\(\frac{h}{2\pi}\)
=> \(\Delta\)x = \(\frac{6.625.10^{-34}}{2\pi.10^6.9,1.10^{-31}}\)=1,16.10-10
VT
28 tháng 10 2017
a) Độ biến thiên động năng của electron đúng bằng công của lực điện trường:
W đ 2 - W đ 1 = 0 - 1 2 m e v 1 2 = A = q e . E . d ⇒ E = - m e v 1 2 2 q e d = 284 . 10 - 5 V / m . .
b) Ta có: v 2 2 - v 1 2 = 2 a s ⇒ a = v 2 2 − v 1 2 2 s = 0 2 − ( 10 4 ) 2 2.0 , 1 = - 5 . 10 7 ( m / s 2 ) .
VT
13 tháng 9 2018
Chọn đáp án A
Từ điều kiện lực hút Cu-lông cân bằng với lực li tâm của chuyển động tròn của electron quanh hạt nhân Hidrô, ta có hệ thức:
18 tháng 12 2014
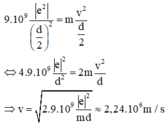
Thầy rất hoan nghênh bạn Thắng đã làm bài tập, cố gắng làm nhiều bài tập hơn nữa để được cộng điểm.
Bài giải của bạn đối với câu hỏi 2 ra kết quả đúng rồi, tuy nhiên cần lưu ý: khi tính độ bất định về vị trí hoặc vận tốc người ta sử dụng hệ thức bất định Heisenberg và thay dấu bất phương trình bằng dấu = để giải cho đơn giản nhé.
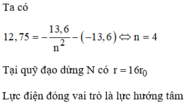
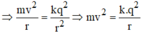
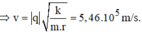
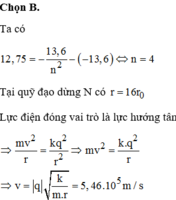
Độ chính xác động lượng \(\Delta Px=m\Delta Vx\).
Thay vào hệ thức Heisenberg \(\Delta x.\Delta Px\ge\frac{h}{2\Pi}\)
=>Độ bất địnhvị trí \(\Delta x\ge\frac{h}{2\Pi.m_e.\Delta Vx}=\frac{6,625.10^{-34}}{2\Pi.9,1.10^{-31}.106}\)=1,09\(^{.10^{-6}}\) m.
câu này áp dụng delta P = m * delta V
delta P * delta V >= h/(2* pi) là ra :)