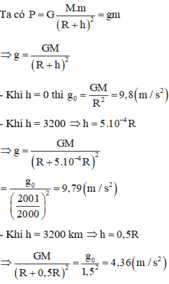Gia tốc rơi tự do ở gần mặt đất g0 = 9,9 m/s2. Tính gia tốc rơi tự do ở độ cao h (với h = R; h = 2R; h = R/2); R: bán kính Trái Đất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
16 tháng 12 2018
Chọn đáp án C
Gia tốc ở mặt đất: 
Gia tốc ở độ cao h: 
m/
s
2
VT
11 tháng 3 2019
Gia tốc ở mặt đất: g = G M R 2 = 10 ( m / s 2 )
Gia tốc ở độ cao h: g h = G M ( R + h ) 2 = G M ( 6 R ) 2 = 0 , 28 m / s 2
30 tháng 11 2021
Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)
HP
25 tháng 12 2020
Trọng lực ở mặt đất \(P=m.g_0=G.\dfrac{m.M}{r^2}\Rightarrow g_0=\dfrac{G.M}{r^2}\)
Lực hấp dẫn của Trái Đất ở độ cao gấp 4 lần bán kính Trái Đất \(F_{hd}=m.g=G.\dfrac{m.M}{25r^2}\Rightarrow g=\dfrac{G.M}{25r^2}\)
\(\Rightarrow\dfrac{g}{g_0}=\dfrac{1}{25}\Rightarrow g=\dfrac{g_0}{25}=\dfrac{9,8}{25}=0,392\left(m/s^2\right)\)
HD
Hà Đức Thọ
Admin
10 tháng 10 2017
Áp dụng công thức:
\(g=g_0.\dfrac{R^2}{(R+h)^2}\)
Trong đó, \(g_0\) là gia tốc trọng trường ở mặt đất.
$R$ là bán kính trái đất.
$h$ là độ cao của vật.
