Dựng ảnh của vật tạo bởi thấu kính hội tụ có tiêu cự f = 4cm, khoảng cách từ vật đến thấu kính bằng 8cm.
Chứng minh: d’ = d; h’ = h, lập công thức: f = (d+d')/4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ảnh ảo, cùng chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{12}=\dfrac{1}{d'}-\dfrac{1}{8}\)
\(\Rightarrow d'=4,8cm\)
Độ cao ảnh A'B':
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{8}{4,8}\Rightarrow h'=1,2cm\)

a) Sử dụng hai trong ba tia đặc biệt để vẽ ảnh.
b) Dựa vào tam giác đồng dạng, suy ra h’ = h; d’ = d = 2f.
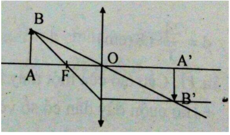

Ta có: Để thu được ảnh thật ngược chiều, nhỏ hơn vật => vật phải cách thấu kính một khoảng d > 2f
Theo đầu bài ta có:
f = 16cm→2f = 32cm
=> Để thu được ảnh nhỏ hơn vật => vật cần đặt cách thấu kính một khoảng
d > 32cm
Đáp án: D

Đáp án C
Khi 0 < d < f, vật ở trong đoạn FO
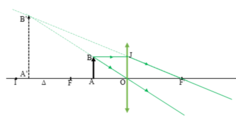
Ảnh là ảo, cùng chiều, lớn hơn vật và nằm ngoài khoảng OF.
Ta có BI = AO = 2f = 2OF’ => OF’ là đường trung bình của ∆B’BI
=> OB’ = OB => ∆A’B’O = ∆ABO => OA’ = OA = 2f và A’B’ = AB
D = d’ = 2f => d + d’ = 4f => f =(d+d')/4