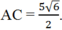Tam giác ABC có góc B = 600; góc C = 450 và AB = 5. Tính độ dài cạnh AC.
A. 5
B. 6
C. 8
D. Đáp án khác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAM có BA=BM và góc ABM=60 độ
nên ΔBAM đều
b: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
=>góc BMD=góc BAD=90 độ
=>DM vuông góc BC

Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
cosC=HC/AC⇒HC=cosC.AC=cos50.35≈22cm
⇒AH=√AC^2−HC^2=√35^2−22^2=√741cm
Trong tam giác vuông AHB ta có:
sinB=AH/AB⇒AB=AH/sinB=√741/sin60=2√247cm
⇒HB=√AB^2−AH^2=√(2√247)^2−741=√247cm
Vậy SABC=AH(HB+HC)/2=√741.(√247+22)/2≈513\(cm^2\)

1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
Chọn D.
Theo định lí hàm sin, ta có
Suy ra: