Cho hình vẽ sau: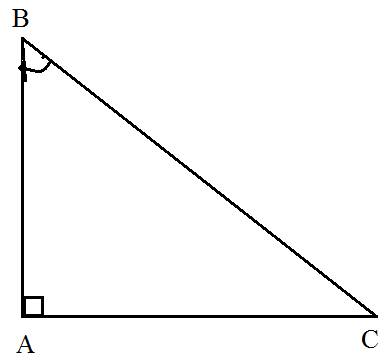
a)Biết AC = 6cm; góc B = 60 độ. Tính BC.
b)Biết AB = 5cm; góc B = 65 độ. Tính BC.
c)Biết AC = 6cm, góc B = 60 độ. Tính AB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
15 tháng 5 2018
Theo tính chất tia phân giác và tính chất dãy tỉ số bằng nhau ta có:
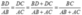
Từ BE//AC nên chứng minh được DABE cân tại B Þ BE = 4cm
28 tháng 3 2021
a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị)
=> MN//BC , theo hệ quả định lý Talet ta có:
AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm)
Nên: (x-6)/x=1,5/6 => x=8(cm)
Nên AB = 8 cm
28 tháng 3 2021
b, AD là đường phân giác của tam giác ABC nên:
AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm)
Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm
=> DC=3 cm
Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong)
Xét △BDE và △CDA có:
∠ACD=∠DBE (c/m tr)
∠ADC=∠BDE (đối đỉnh)
=> △BDE=△CDA (g.g)
=> BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm)
Vậy: BD= 2 cm
BE= 4 cm
ML
2
21 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có AC<AB<BC(6cm<8cm<10cm)
mà góc đối diện với cạnh AC là \(\widehat{ABC}\)
góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh CB là \(\widehat{BAC}\)
nên \(\widehat{ABC}< \widehat{ACB}< \widehat{BAC}\)
b) Xét ΔAMB và ΔCMD có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔAMB=ΔCMD(c-g-c)
11 tháng 11 2021
Áp dụng PTG: \(BC^2=AB^2+AC^2=100\Rightarrow BC=10\left(cm\right)\)
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
SL
3
5 tháng 9 2021
Cái này vẽ dễ nên bạn có thể lấy thước ra và đo rồi vẽ mà nhỉ?
3 tháng 10 2021
Áp dụng Pytago: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(AH\cdot BC=AC\cdot AB\Leftrightarrow AH=\dfrac{8\cdot6}{10}=4,8\left(cm\right)\)
NB
1
a) \(BC=\dfrac{AC}{sinB}=\dfrac{6}{sin60}=4\sqrt{3}\left(cm\right)\)
b) \(BC=\dfrac{AB}{cosB}=\dfrac{5}{cos65}\approx11,831\left(cm\right)\)
c) \(AB=\dfrac{AC}{tanB}=\dfrac{6}{tan60}=2\sqrt{3}\left(cm\right)\)