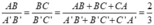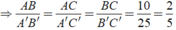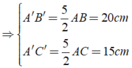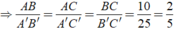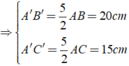cho tam giác ABC = tam giác A'B'C'. Biết góc BC = 10cm; góc AB : góc AC = 4 : 3 và góc AB + góc AC = 14cm. Tính các cạnh của tam giác A'B'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có
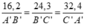
a) Tính được A'B' = 6,2cm. Từ đó tính được B'C' = 9,3cm và A'C' = 12,4cm.
b) Tương tự câu a tính được A'B' = 26,2cm, B'C' = 39,3cm và A'C' = 52,4cm

2. \(\Delta ABC\)có AB=AC \(\Rightarrow\Delta ABC\)cân.
AD là phân giác \(\Delta ABC\)mà \(\Delta ABC\)cân.
\(\Rightarrow AD\)l là đường trung trực \(\Delta ABC\)..
\(\Rightarrow AD\)là đường cao \(\Delta ABC\)..
\(\Leftrightarrow AD\perp BC\).

ΔABC đồng dạng với ΔA'B'C'
=>A'B'/AB=B'C'/BC=A'C'/AC
=>A'B'/162=B'C'/243=A'C'/327
=>A'B'/54=B'C'/81=A'C'/109

a) Làm theo bạn Doan Thanh phuong nhé!
b) Ta có: A = 90o => Tam giác ABC vuông tại a.
Áp dụng định lý Pitago. Ta có:
\(AB^2+AC^2=BC^2\Leftrightarrow3^2+4^2=9+16=25\)
\(\Rightarrow BC^2=25\). Mà \(25=5^2\Rightarrow BC=5\) cm
a) Xét tam giác ABC và tam giác A'B'C' có :
\(\widehat{A}=\widehat{A'}\left(gt\right)\)
AB = A'B' ( gt )
AC = A'C' ( gt )
Suy ra tam giác ABC = tam giác A'B'C' ( c - g - c )
b) Ta có tam giác ABC vuông tại A ( gt )
=> AB2 + AC2 = BC2 ( định lý Py-ta-go )
hay 32 + 42 = BC2
BC2 = 32 + 42 = 9 + 16 = 25
=> BC = 5