Biết AB//CD,AD//BC;góc A1=4lần góc B2. Góc C1 bằng bao nhiêu?
Các bạn nhớ ghi cách làm luôn nha! Mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AN
0
CM
1 tháng 11 2017
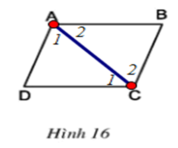
Hình thang ABCD có đáy AB, CD ⇒ AB // CD ⇒ ∠A2 = ∠C1 ̂ (hai góc so le trong)
Lại có: AD // BC ⇒ ∠A1 = ∠C2 (hai góc so le trong)
Xét ΔABC và ΔCDA có:
∠A2 = ∠C1 (cmt)
AC chung
∠A1 = ∠C2 (cmt)
⇒ ΔABC = ΔCDA (g.c.g)
⇒ AD = BC, AB = CD (các cặp cạnh tương ứng)
b)
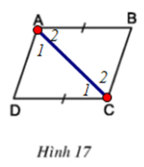
Xét ΔABC và ΔCDA có:
AC chung
∠A2 = ∠C1 (cmt)
AB = CD
⇒ ΔABC = ΔCDA (c.g.c)
⇒ AD = BC (hai cạnh tương ứng)
∠A1 = ∠C2 (hai góc tương ứng) ⇒ AD // BC (hai góc so le trong bằng nhau)
5 tháng 1 2018
a.Cho tứ giác ABCD biết AB//CD và AB=CD.CMR AD//BC và AD=BC
Ta có :\(\left\{{}\begin{matrix}\text{AB // CD}\\AB=CD\end{matrix}\right.\)(gt)
=> Tứ giác ABCD là hình bình hành
=> \(\left\{{}\begin{matrix}\text{AD //BC}\\AD=AD\end{matrix}\right.\)(tính chất hình bình hành)
b.Cho tứ giác ABCD biết AB//CD và AD//BC.CMR:AB=CD và AD=BC
Ta có : \(\left\{{}\begin{matrix}\text{AB //CD}\\\text{AD //BC}\end{matrix}\right.\) (gt)
=> Tứ giác ABCD là hình bình hành
Do đó : \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\)(tính chất hình bình hành)
c.Cho tứ giác ABCD biết AB=CD và AD=BC.CMR AD//BC và AD//BC
Ta có : \(\left\{{}\begin{matrix}AB=CD\\AD=BC\end{matrix}\right.\) (gt)
=> Tứ giác ABCD là hình bình hành
=> AD //BC (tính chất hình bình hành)
*Bạn cũng có thể xét các tứ giác là hình vuông, hình chữ nhật cũng có tính chất tương tự.
KT
3 tháng 8 2018
tự vẽ hình
a) Xét tam giác DAC và tam giác BCA có:
góc DAC = góc BCA (slt do AD // BC)
AC: chung
góc DCA = góc BAC (slt do AB // DC)
suy ra: tam giác DAC = tam giác BCA (g.c.g)
=> AD = BC; DC = AB
b) Xét tam giác DAC và tam giác BCA có:
AD = AB
góc DCA = góc BAC (slt do AB // CD)
AC: chung
suy ra: tam giác DAC = tam giác BCA (c.g.c)
=> AD = BC
góc DAC = góc BCA
mà 2 góc này slt
=> AD // BC
29 tháng 5 2016
a) Ta có : AB // CD ( do ABCD là hình thang )
AD // BC ( gt )
=> ABCD là hình bình hành
=> AD = BC ; AB = CD
b) Ta có : AB = CD ( gt )
AB // CD ( gt )
=> ABCD là hình bình hành
=> AD // BC ; AD = BC
31 tháng 7 2022
a: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đo: ABCD là hình bình hành
Suy ra:AB=CD và AD=BC
b: Xét tứ giác ABCD có
AB//CD
AB=CD
Do đó; ABCD là hình bình hành
Suy ra: AD//BC và AD=BC
QN
22 tháng 8 2017
a) Kẻ đoạn thẳng AC.
Ta có: AB // CD (ABCD là hình thang)
Xét \(\Delta ABC\) và \(\Delta DCA\), có:
\(\widehat{BAC} = \widehat{ACD}\) (hai góc so le trong, AB//CD)
AC là cạnh chung
\(\widehat{DAC} = \widehat{BCA}\) (hai góc so le trong, AD // BC)
Vậy \(\Delta ABC=\Delta CDA\) (g.c.g)
\(\Rightarrow AD=BC;AB=CD\) (ĐPCM)
b) Xét \(\Delta ADC\) và \(\Delta CBA\), có:
AB = CD (gt)
\(\widehat{BAC} = \widehat{ACD}\) ((hai góc so le trong, AB//CD)
AC là cạnh chung
\(\Rightarrow\Delta ADC=\Delta CBA\) (c.g.c)
\(\Rightarrow\) \(\widehat{DAC} = \widehat{BCA}\) (hai góc tương ứng), mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AD // BC
Ta có: \(\Delta ADC=\Delta CBA\) \(\Rightarrow\) AD = BC (hai cạnh tương ứng)
Vậy AD // BC, AD = BC (đpcm)
HV
2
HL
10 tháng 10 2019
Vì ABCD là hình thang có đáy AB,CD và AB=CD=>ABCD là hình thang=>BC=AD,BC//AD.
chúc bạn học tốt nhớ k cho mình nha!
10 tháng 10 2019
Hình thang ABCD có AB=CD và AB//CD nên hình thang ABCD là hình bình hành.
=> \(BC=AD,BC//AD\)
HV
0
DP
2
26 tháng 3 2017
xét tứ giác ABCD có: AB//CD (2 đáy của hình thang) ;
AD//BC(gt) => ABCD là hình bình hành => AD =BC; AB= CD (t/c hbh)
Góc Â1 và B1 với C1 là góc nào???????????????????????????????????????????????????????????????????????????????????????????????????????????