Cho hàm số y = f[x] = 2x - 5
a. Tính f[-2]; f[1]
b. Tìm x để f[x] = -11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x
Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x

Answer:
a)
\(y=f\left(x\right)=\frac{1}{2}x-\frac{1}{2}\)
Tính \(f\left(-3\right)\): \(\frac{1}{2}.\left(-3\right)-\frac{1}{2}=\frac{-3}{2}-\frac{1}{2}=-2\)
Tính \(f\left(\frac{3}{4}\right)\) : \(\frac{1}{2}.\frac{3}{4}-\frac{1}{2}=\frac{3}{8}-\frac{1}{2}=\frac{-1}{8}\)
b)
\(\frac{1}{2}x-\frac{1}{2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{2}x=\frac{1}{2}+\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{2}x=1\)
\(\Leftrightarrow x=1:\frac{1}{2}\)
\(\Leftrightarrow x=2\)

a) a = 2
+ y = f(1) = 2.1 = 2
+ y = f(-2) = 2.(-2) = -4
+ y = f(-4) = 2.(-4) = -8
b) f(2) = 4
=> 4 = a.2
=> a = 2
( Vẽ đồ thị hàm số thì bạn tự vẽ được mà :)) Ở đây vẽ hơi khó )
c) Khi a = 2
=> Ta có đồ thị hàm số y = 2x
+ A(1;4)
=> xA = 1 ; yA = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2.1 ( vô lí )
=> A không thuộc đồ thị hàm số y = 2x
+ B = ( -1; -2 )
=> xB = -1 ; yB = -2
Thế vào đồ thị hàm số y = 2x ta có :
-2 = 2(-1) ( đúng )
=> B thuộc đồ thị hàm số y = 2x
+ C(-2; 4)
=> xC = -2 ; yC = 4
Thế vào đồ thị hàm số y = 2x ta có :
4 = 2(-2) ( vô lí )
=> C không thuộc đồ thị hàm số y = 2x
+ D(-2 ; -4 )
=> xD = -2 ; yD = -4
Thế vào đồ thị hàm số y = 2x ta có :
-4 = 2(-2) ( đúng )
=> D thuộc đồ thị hàm số y = 2x

Ta có y=f(x)-2x
* f(1)=-2.1=-2
* f(1/2)=-2.1/2=-1
* f(3)=-2.3=-6
k mình nha mình làm nhanh nhất

Đáp án A
Ta có
![]()
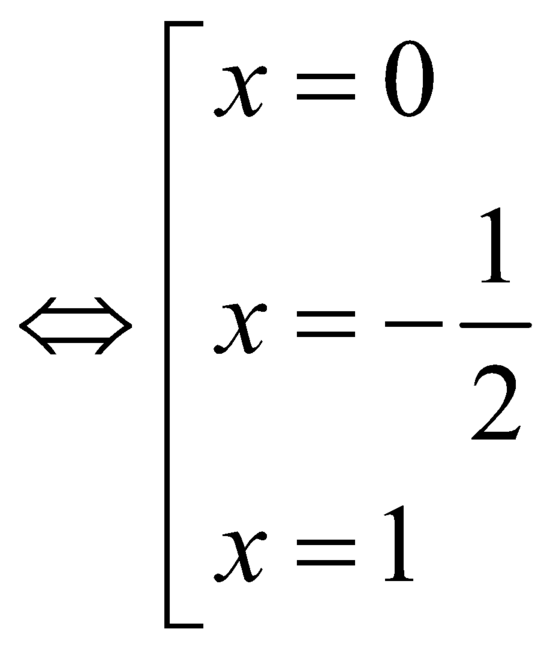 .
.
Bảng xét dấu:
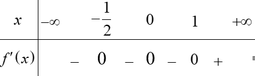
Suy ra hàm số có một điểm cực trị.

Mình thiếu kết luận câu b nha bạn!
Vậy đường thẳng OA là đồ thị của hàm số y = -2x.
a)f(-2)=2.(-2)-5=-9
f(1)=2.1-5=-3
b) Để f(x)=-11
Ta có: 2.x-5=-11
2x=-11+5
2.x=-6
x =-6:2
x=-3
Vậy để f(x)=11 thì x=-3