Cho mạch điện có sơ đồ như hình 5.6, trong đó điện trở R 1 = 6Ω; dòng điện mạch chính có cường độ I = 1,2A và dòng điện đi qua điện trở R 2 có cường độ I 2 = 0,4A. Tính hiệu điện thế U đặt vào hai đầu đoạn mạch
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 8 2019
R 1 và R 2 mắc song song nên:
I = I 1 + I 2 → I 1 = I - I 2 = 1,2 – 0,4 = 0,8A
Và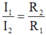 
Và U = U 2 = U 1 = I 1 . R 1 = 0,8.6 = 4,8V
→ Điện trở
R
2
là: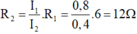 
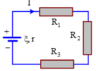
VT
15 tháng 1 2018
Vì R 3 song song với R 1 và R 2 nên:
U = U 1 = U 2 = U 3 = 4,8V
I = I 1 + I 2 + I 3 → I 3 = I - I 1 - I 2 = 1,5 – 0,8 – 0,4 = 0,3A
Điện trở
R
3
bằng: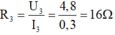 
Điện trở tương đương của toàn mạch là: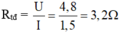 
TL
18 tháng 6 2018
Theo định luật Ôm : \(I=\dfrac{U}{R}\)
=> \(U_1=R_1.I_1=7,2V\)
Không có hình cụ thể thì cho giả định : \(U_1=U_{tm}=7,2V\)
Điện trở R2 là :
\(I_2=\dfrac{U_{tm}}{R_2}=>R_2=\dfrac{U_{tm}}{I_2}=18\Omega\)
22 tháng 6 2018
Tóm tắt:
R1 = 6ohm
I = 1,2A
I2 = 0,4A
------------------
R2 =?ohm
Giai:
Vì I khác I2 (1,2 khác 0,4) nên đây là đoạn mạch song song.
Cường độ dòng điện đi qua điện trở R1 là:
I = I1 + I2 => I1 = I - I2 = 1,2 - 0,4 = 0,8 (A)
Vì là mạch song song nên ta có:
U1 = U2 hay I1.R1 = I2.R2 => R2 = (I1.R1)/I2 = (0,8.6)/0,4 = 12 (om)
Vậy điện trở R2 là 12ohm.
N
25 tháng 11 2021
a. \(U=U1=U2=I1\cdot R1=\left(1,4-0,6\right)\cdot8=6,4V\left(R1//R2\right)\)
\(\Rightarrow R2=U2:I2=6,4:0,6=\dfrac{32}{3}\Omega\)
b. \(U=U1=U2=6,4V\left(R1//R2\right)\)
VT
18 tháng 6 2018
Công suất tiêu thụ ở mạch ngoài
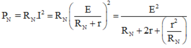
Để công suất mạch ngoài cực đại (Pmax) thì mẫu số của biểu thức trên phải đạt cực tiểu
tức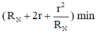 
Áp dụng bất đẳng thức Cô-si cho 2 số dương RN và r2/RN
Ta có:
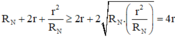
Dấu bằng xảy ra khi RN = r
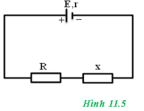
⇒ Rx = RN – R = r – R = 1,1 – 0,1 = 1Ω
Giá trị cực đại của công suất mạch ngoài:
VT
6 tháng 4 2018
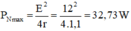
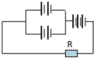
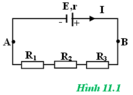
a) Các điện trở hình 11.1 được mắc nối tiếp với nhau nên điện trở tương đương của mạch ngoài là: RN = R1 + R2 + R3 = 5 + 10 + 13 = 18ω
b) Cường độ dòng điện I chạy qua nguồn:
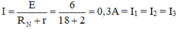
Hiệu điện thế mạch ngoài: UN = I.RN = 18.0,3 = 5,4V
c) Hiệu điện thế giữa hai đầu điện trở R1 là: U1 = R1.I = 5.0,3 = 1,5V
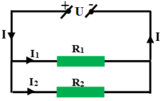
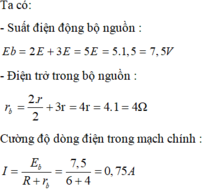
Hiệu điện thế U đặt vào hai đầu đoạn mạch là:
U = U 1 = U 2 = I 2 . R 2 = 0,4.12 = 4,8V