cho tam giác có độ dài ba cạnh là a;b;c.Chứng minh: a^2(b+c-a)+b^2(a+c-b)+c^2(a+b-c)<=3abc
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


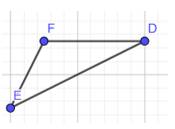
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
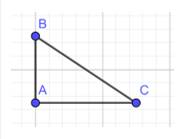
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A

a) gọi 3 cạnh của tam giác lần lượt là a;b;c ta có
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và a+b+c =60
áp dụng tích chất của dãy tỉ số bằng nhau ta có
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
\(\frac{a}{3}=5=>a=15\)
\(\frac{b}{4}=5=>b=20\)
\(\frac{c}{5}=5=>c=25\)
a, Gọi 3 cạnh của tam giác lần lượt là x, y, t
Ta có: \(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}\)và \(x+y+t=60\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{3}=\frac{y}{4}=\frac{t}{5}=\frac{x+y+t}{3+4+5}=\frac{60}{2}=5\)
\(\frac{x}{3}=5\Rightarrow a=15\)
\(\frac{y}{4}=5\Rightarrow a=20\)
\(\frac{t}{5}=5\Rightarrow a=25\)

a: Vì 4cm+5cm=9cm<10cm
nên đây không là bộ ba độ dài của một tam giác
b: Vì 3cm+5cm=8cm
nên 3cm;5cm;8cm không là độ dài 3 cạnh của tam giác
c: Vì 4+6=10>8 và 4+8>6 và 6+8>4
nên đây là độ dài ba cạnh của một tam giác


a) Đặt độ dài cạnh AB là x (\(x > 0\))
Theo giả thiết ta có độ dài \(AC = AB + 2 = x + 2\)
Áp dụng định lý pitago trong tam giác vuông ta có
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{x^2} + {{\left( {x + 2} \right)}^2}} = \sqrt {2{x^2} + 4x + 4} \)
b) Chu vi của tam giác là \(C = AB + AC + BC\)
\( \Rightarrow C = x + \left( {x + 2} \right) + \sqrt {2{x^2} + 4x + 4} = 2x + 2 + \sqrt {2{x^2} + 4x + 4} \)
Theo giả thiết ta có
\(\begin{array}{l}C = 24 \Leftrightarrow 2x + 2 + \sqrt {2{x^2} + 4x + 4} = 24\\ \Leftrightarrow \sqrt {2{x^2} + 4x + 4} = 22 - 2x\\ \Rightarrow 2{x^2} + 4x + 4 = {\left( {22 - 2x} \right)^2}\\ \Rightarrow 2{x^2} + 4x + 4 = 4{x^2} - 88x + 484\\ \Rightarrow 2{x^2} - 92x + 480 = 0\end{array}\)
\( \Rightarrow x = 6\) hoặc \(x = 40\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {2{x^2} + 4x + 4} = 22 - 2x\) ta thấy chỉ có \(x = 6\) thỏa mãn phương trình
Vậy độ dài ba cạnh của tam giác là \(AB = 6;AC = 8\) và \(BC = 10\)(cm)

Hai lần chu vi tam giác ABC là : 18,25 + 23,55 + 20,3 = 62,1 ( cm )
Giải thích : Cạnh 1 + Cạnh 2 + Cạnh 2 + Cạnh 3 + Cạnh 1 + Cạnh 3 = 62,1 nên 62,1 là 2 lần chu vi
Chu vi tam giác ABC là : 62,1 : 2 = 31,05 ( cm )
Đáp số : 31,05 cm.
OK,k mik nha

2 lần chu vi ABC là:18,25+23,55+20,3=62,1(cm)
Chu vi tam giác ABC là:62,1:2=31,05(cm)
ok,tick nha

2: BC=căn 6^2+8^2=10cm
3:
a: 5cm; 12cm; 9cm
5+12>9; 5+9>12; 12+9>5
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
b: 12+16>20; 12+20>16; 20+16>12
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
4:
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
10:
a: AB=căn 10^2-6^2=8cm
b: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
c: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB//CD