Tìm các chữ số a;b;c sao cho : abc + 2 = 11 x ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
14 tháng 11 2021
b) để a4b ⋮ 2 và 5
thì b=0
để a40 ⋮ 3 và 9 thì tổng các chữ số phải ⋮ 9
⇒ \(\left(a+4\right)\text{⋮}9\)
⇒ \(a=5\)
Vậy a=5, b=0
c) để 2a5b ⋮5 thì b=0 hoặc 5
Nếu b=0 thì a=2
Nếu b=5 thì a=7
Vậy (a,b)=\(\left\{\left(2;0\right);\left(7;5\right)\right\}\)
15 tháng 11 2023
Bài 7:
a: \(24=2^3\cdot3\)
b: \(75=5^2\cdot3\)
c: \(300=2^2\cdot3\cdot5^2\)
d: \(520=2^3\cdot5\cdot13\)
Bài 6:
a:
Sửa đề: 56ab
Đặt \(X=\overline{56ab}\)
X chia hết cho 2 và 5 nên X chia hết cho 10
=>X có tận cùng là 0
=>b=0
=>\(X=\overline{56a0}\)
X chia hết cho 3 và 9 nên X chia hết cho 9
=>5+6+a+0 chia hết cho 9
=>a+11 chia hết cho 9
=>a=7
=>X=5670
b: Đặt \(X=\overline{3ab}\)
X chia hết cho 2 và 5 nên X chia hết cho 10
=>b=0
=>\(X=\overline{3a0}\)
X chia hết cho 3 và 9 nên X chia hết cho 9
=>3+a+0 chia hết cho 9
=>a=6
=>X=360
c: Đặt \(X=\overline{1a2b}\)
X chia hết cho 5 nên b=0 hoặc b=5
TH1: b=0
=>\(X=\overline{1a20}\)
X chia hết cho 9
=>1+a+2+0 chia hết cho 9
=>a+3 chia hết cho 9
=>a=6
=>X=1620
TH2: b=5
=>\(X=\overline{1a25}\)
X chia hết cho 9
=>1+a+2+5 chia hết cho 9
=>a+8 chia hết cho 9
=>a=1
=>X=1125
30 tháng 10 2023
a: 0,1246
b:
Sửa đề: Có tích các chữ số bằng 48
Số cần tìm là 8,321
5 tháng 4 2018
a tích các chữ số có 1 chữsố bằng 120 là
120 = 3x5x8
vậy số tự nhiên bé nhất có tích là 120 là 385
nhớ kic cho mik nhé
nhưng bài này sai thôi tớ ko biết đâu
VN
2
VD
19 tháng 9 2016
- ta có 10a + b +10b +a =176
<=> 10(a+b) +a +b =176
<=> 11(a+b) =176
<=> a + b =16
=> a=7 và b=9 hoặc a=9 và b=7 (vì a khác b)
- Theo đề ta có : c+b=c =>b=0
Vì ac và cb là số có hai chữ số => a=1
=> 10 +c +10c = 100 + c
=> 10c = 90
=>c=9
Vậy số cần tìm là 109
19 tháng 9 2016
Bài 1:
Giải:
Ta có:
\(\overline{ab}+\overline{bc}=176\)
\(\Rightarrow10a+b+10b+a=176\)
\(\Rightarrow11a+11b=176\)
\(\Rightarrow11\left(a+b\right)=176\)
\(\Rightarrow a+b=16\)
Vì a, b là chữ số nên ta có bảng sau:
| a | 7 | 9 | 8 |
| b | 9 | 7 | 8 |
Vậy các cặp số \(\left(a;b\right)\) là: \(\left(7;9\right);\left(9;7\right);\left(8;8\right)\)
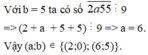
\(abc+2=11×ab\)
\(ab×10+c+2=11×ab\)
\(c+2=ab\)
Vì \(c\)là chữ số mà \(ab\)là số có 2 chữ số nên \(c\)chỉ nhận các giá trị là: 8 và 9
Ta có 2 TH sau:
TH1: \(c=8\)
\(\Rightarrow ab=8+2=10\)
TH2: \(c=9\)
\(\Rightarrow ab=9+2=11\)
Vậy ta có 2 cặp \(\left(a,b,c\right)\)là \(\left(1,0,8\right);\left(1,1,9\right)\)