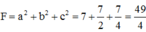Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số thực dương thay đổi sao cho a2 + 4b2 + 16c2 = 49. Tính tổng F = a2 + b2 +c2 sao cho khoảng cách từ O đến (ABC) là lớn nhất.
A. F = 51 5
B. F = 51 4
C. F = 49 5
D. F = 49 4


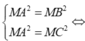
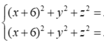
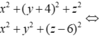



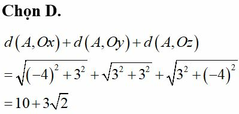

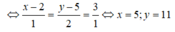
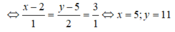
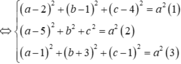
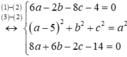
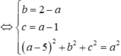
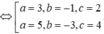
Đáp án D
Phương pháp:
- Phương trình đoạn chắn của mặt phẳng đi qua 3 điểm
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c khác 0): x a + y b + z c = 1
- Sử dụng bất đẳng thức: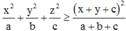

Đẳng thức xảy ra khi và chỉ khi x a = y b = z c
Cách giải:
A(a;0;0), B(0;b;0), C(0;0;c). (a, b,c > 0)
Mặt phẳng (ABC) có phương trình: x a + y b + z c = 1
Khoảng cách từ O đến (ABC):
Ta có: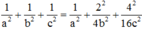
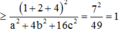
Dấu “=” xảy ra khi và chỉ khi:
=>