Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) qua hai điểm M(1;8;0)⸦C(0;0;3) cắt các nửa trụ dương Ox,Oy lần lượt tại A, B sao cho OG nhỏ nhất (G là trọng tâm tam giác ABC). Biết G(a;b;c) tính P=a+b+c
A. 12
B. 6
C. 7
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Phương trình đường thẳng d qua M vuông góc với (P) là 
Gọi H = d ∩ (P) => H (0; 1; -1).
M' đối xứng với M qua (P) nên H là trung điểm MM' => M’ (-4; 0; -3)

Gọi n p → ; n Q → lần lượt là các VTPT của (P) và (Q) ta có
![]()
Khi đó ta có
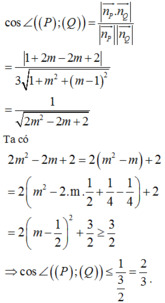
Dấu “=” xảy ra
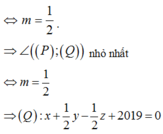
Khi đó (Q) đi qua điểm
Chọn C.

Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
Chọn đáp án B.