Cho a = log 2 7 ; b = log 5 7 . Giá trị của log 7 bằng
A.![]()
B. ![]()
C. a + b
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

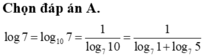
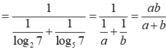

Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)

\(a,A=log_23\cdot log_34\cdot log_45\cdot log_56\cdot log_67\cdot log_78\\ =log_28\\ =log_22^3\\ =3\\ b,B=log_22\cdot log_24...log_22^n\\ =log_22\cdot log_22^2...log_22^n\\ =1\cdot2\cdot...\cdot n\\ =n!\)

\(log_{12}21=\dfrac{log_321}{log_312}=\dfrac{log_3\left(7\cdot3\right)}{log_3\left(2^2\cdot3\right)}=\dfrac{log_37+log_33}{log_34+log_33}\)
\(=\dfrac{log_37+1}{log_32^2+1}=\dfrac{log_37+1}{2\cdot log_32+1}=\dfrac{b+1}{2a+1}\)

a: \(log_2\left(mn\right)=log_2\left(2^7\cdot2^3\right)=7+3=10\)
\(log_2m+log_2n=log_22^7+log_22^3=7+3=10\)
=>\(log_2\left(mn\right)=log_2m+log_2n\)
b: \(log_2\left(\dfrac{m}{n}\right)=log_2\left(\dfrac{2^7}{2^3}\right)=7-3=4\)
\(log_2m-log_2n=log_22^7-log_22^3=7-3=4\)
=>\(log_2\left(\dfrac{m}{n}\right)=log_2m-log_2n\)
a) \(\log_2\left(mn\right)=\log_2\left(2^7.2^3\right)=\log_22^{7+3}=\log_22^{10}=10.\log_22=10.1=10\)
\(\log_2m+\log_2n=\log_22^7+\log_22^3=7\log_22+3\log_22=7.1+3.1=7+3=10\)
b) \(\log_2\left(\dfrac{m}{n}\right)=\log_2\dfrac{2^7}{2^3}=\log_22^4=4.\log_22=4.1=4\)
\(\log_2m-\log_2n=\log_22^7-\log_22^3=7.\log_22-3\log_22=7.1-3.1=4\)

\(log_3\sqrt{3}=log_33^{\dfrac{1}{2}}=\dfrac{1}{2}\)
\(lne^3=log_ee^3=3\)
\(log_{27}3=log_{3^3}3=\dfrac{1}{3}\)
\(\log_{\sqrt{3}}3=log_{3^{\dfrac{1}{2}}}3=1:\dfrac{1}{2}=2\)
\(\log_{0,125}2=log_{2^{-3}}2=\dfrac{1}{-3}\)
\(\log_{\sqrt[3]{49}}7=\log_{7^{\dfrac{2}{3}}}7=1:\dfrac{2}{3}=\dfrac{3}{2}\)
\(\log_{\dfrac{1}{125}}5=\log_{5^{-3}}5=-\dfrac{1}{3}\)
\(\log_84=log_{2^3}2^2=\dfrac{1}{3}\cdot2=\dfrac{2}{3}\)
\(\log_{25}\left(\dfrac{1}{5}\right)=\log_{5^2}5^{-1}=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(\log_{\dfrac{1}{5}}\sqrt{5}=\log_{5^{-1}}5^{\dfrac{1}{2}}=\dfrac{1}{-1}\cdot\dfrac{1}{2}=-\dfrac{1}{2}\)
\(log_{\dfrac{1}{7}}\sqrt[5]{49}=\log_{7^{-1}}7^{\dfrac{2}{5}}=\dfrac{1}{-1}\cdot\dfrac{2}{5}=-\dfrac{2}{5}\)
\(\log_4\left(\dfrac{1}{\sqrt{2}}\right)=\log_{2^2}\left(\sqrt{2}\right)^{-1}\)
\(=\log_{2^{-2}}\left(\sqrt{2}\right)^{-\dfrac{1}{2}}=\dfrac{1}{-2}\cdot\dfrac{-1}{2}=\dfrac{1}{4}\)
\(\log_{27}3\sqrt{3}=\log_{3^3}3^{\dfrac{3}{2}}=\dfrac{1}{3}\cdot\dfrac{3}{2}=\dfrac{1}{2}\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B


Đáp án D.
Ta có
log 6125 7 = log 6125 + log 7 = log 7 2 . 125 + 1 2 log 7
= 5 2 log 7 + log 5 3 = 5 2 n + 3 log 5 = 5 2 n + 3 1 - log 2
= 5 2 n + 3 - 3 m .


a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\) (ĐK: \(x + 1 > 0;2 - x > 0 \Leftrightarrow - 1 < x < 2\))
\(\begin{array}{l} \Leftrightarrow {\log _{{7^{ - 1}}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow - {\log _7}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\log _7}{\left( {x + 1} \right)^{ - 1}} > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\left( {x + 1} \right)^{ - 1}} > 2 - x\\ \Leftrightarrow \frac{1}{{x + 1}} - 2 + x > 0\\ \Leftrightarrow \frac{{1 + \left( {x - 2} \right)\left( {x + 1} \right)}}{{x + 1}} > 0\\ \Leftrightarrow \frac{{1 + {x^2} - x - 2}}{{x + 1}} > 0 \Leftrightarrow \frac{{{x^2} - x - 1}}{{x + 1}} > 0\end{array}\)
Mà – 1 < x < 2 nên x + 1 > 0
\( \Leftrightarrow {x^2} - x - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}x < \frac{{1 - \sqrt 5 }}{2}\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
KHĐK ta có \(\left[ \begin{array}{l} - 1 < x < \frac{{1 - \sqrt 5 }}{2}\\\frac{{1 + \sqrt 5 }}{2} < x < 2\end{array} \right.\)
b) \(2\log \left( {2x + 1} \right) > 3\) (ĐK: \(2x + 1 > 0 \Leftrightarrow x > \frac{{ - 1}}{2}\))
\(\begin{array}{l} \Leftrightarrow \log \left( {2x + 1} \right) > \frac{3}{2}\\ \Leftrightarrow 2x + 1 > {10^{\frac{3}{2}}} = 10\sqrt {10} \\ \Leftrightarrow x > \frac{{10\sqrt {10} - 1}}{2}\end{array}\)
KHĐK ta có \(x > \frac{{10\sqrt {10} - 1}}{2}\)