Với giá trị nào của x thì ta có: a) |x| + x = 0 ; b) x + |x| = 2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 6 2017
+) Với x ≥ 0 thì |x| = x nên ta có: x + x = 0 ⇒ 2x = 0 ⇒ x = 0
+) Với x < 0 thì |x| = -x nên ta có: -x + x = 0 ⇒ 0 = 0 (luôn đúng)
⇒ |x| + x = 0 luôn có nghiệm đúng với x < 0
Vậy với x ≤ 0 thì |x| + x = 0.
BT
0
NH
2
PT
1
PT
1
PT
1
CM
22 tháng 10 2017
Vẽ hình:
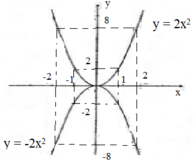
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.
CM
28 tháng 6 2017
Vẽ hình:
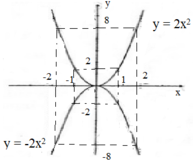
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
LN
1
17 tháng 2 2022
a, Để \(\left|x\right|+x=0\)thì x < 0
b, Để \(x+\left|x\right|=2x\)thì x > 0
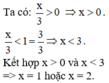
a) x = 0
b ) x = 1
a) x = (...;-3;-2;-1;0)
b) x = (1;2;3;4,..)