1. a) Chứng minh rằng tổng của một phân số dương với số nghịch đảo của nó lớn hơn hoặc bằng 2;
b) Áp dụng để chứng tỏ rằng nếu x, y, z là các số nguyên cùng dương hoặc cùng âm, thì:
P =\(\frac{3x}{y}\)+ \(\frac{3y}{x}\) > hoặc = 6
Q = \(\frac{3x}{y}\)+\(\frac{3y}{x}\)+ \(\frac{3x}{z}\)+\(\frac{3z}{x}\)+ \(\frac{3y}{z}\)+ \(\frac{3z}{y}\)> hoặc =

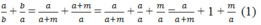
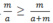 (dấu "=" xảy ra khi m = 0)
(dấu "=" xảy ra khi m = 0)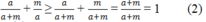
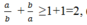 , (dấu "=" xảy ra khi m = 0 hay a = b )
, (dấu "=" xảy ra khi m = 0 hay a = b )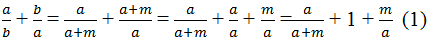
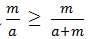 (dấu "=" xảy ra khi m = 0)
(dấu "=" xảy ra khi m = 0)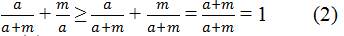
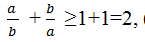 , (dấu "=" xảy ra khi m = 0 hay a = b )
, (dấu "=" xảy ra khi m = 0 hay a = b )
1a) Không giảm tính tổng quát, giả sử \(a\ge b\) suy ra \(a=b+m\) \(\left(m\ge0\right)\)
Ta có \(\frac{a}{b}+\frac{b}{a}=\frac{b+m}{b}+\frac{b}{b+m}\)
\(=1+\frac{m}{b}+\frac{b}{b+m}\ge1+\frac{m}{b+m}+\frac{b}{b+m}=\frac{b+m}{b+m}=1+\frac{b+m}{b+m}\)
\(=1+1=2\)
Vậy \(\frac{a}{b}+\frac{b}{a}\ge2\) (dấu \(=\Leftrightarrow m=0\Leftrightarrow a=b\))
Vậy tổng của một phân số dương với số nghịch đảo của nó lớn hơn hoặc bằng 2.
a)Tham khảo:Câu hỏi của Yêu Chi Pu - Toán lớp 6 - Học toán với OnlineMath
b) \(P=\frac{3x}{y}+\frac{3y}{x}=3\left(\frac{x}{y}+\frac{y}{x}\right)\ge3.2=6\)
\(Q=3\left(\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}\right)\ge3\left(2+2+2\right)=18\)