Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
Bài 1:
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó:ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KDB}=\widehat{KEC}\)
Xét ΔKDB và ΔKEC có
\(\widehat{KDB}=\widehat{KEC}\)
BD=CE
\(\widehat{KBD}=\widehat{KCE}\)
Do đó: ΔKDB=ΔKEC
tham khảo
https://hoc24.vn/hoi-dap/tim-kiem?id=561093&q=Cho%20tam%20gi%C3%A1c%20ABC%20c%C3%A2n%20t%E1%BA%A1i%20A%20.%20%C4%90i%E1%BB%83m%20D%20thu%E1%BB%99c%20c%E1%BA%A1nh%20AB%20%2C%20%C4%91i%E1%BB%83m%20E%20thu%E1%BB%99c%20c%E1%BA%A1nh%20AC%20sao%20cho%20AD%20%3D%20AE%20.%20G%E1%BB%8Di%20K%20l%C3%A0%20giao%20%C4%91i%E1%BB%83m%20c%E1%BB%A7a%20BE%20v%C3%A0%20CD%20.%20Ch%E1%BB%A9ng%20minh%20r%E1%BA%B7ng%20%20%20a%29%20BE%20%3D%20CD%20%20b%29%20Tam%20gi%C3%A1c%20KBD%20b%E1%BA%B1ng%20tam%20gi%C3%A1c%20KCE%20%20c%29%20AK%20l%C3%A0%20ph%C3%A2n%20gi%C3%A1c%20c%E1%BB%A7a%20g%C3%B3c%20A%20%20d%29%20Tam%20gi%C3%A1c%20KBC%20c%C3%A2n
a: Xét ΔAEBvà ΔADC có
AE=AD
góc A chung
AB=AC
=>ΔAEB=ΔADC
=>BE=CD
b: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
c: Xét ΔAMB và ΔAMC có
MA chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
`@`` \text {dnv}`
`a,`
Xét `\Delta ABE` và `\Delta ACD`:
`\text {AB = AC (Tam giác ABC cân tại A)}`
`\hat {A}`` \text {chung}`
`\text {AD = AE (gt)}`
`=> \Delta ABE = \Delta ACD (c-g-c)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Vì `\Delta ABE = \Delta ACD (a)`
$ -> \widehat {ACD} = \widehat {ABE} (\text {2 góc tương ứng})$
`->` $\widehat {ADC} = \widehat {AEB} (\text {2 góc tương ứng})$
Ta có: \(\left\{{}\begin{matrix}\widehat{ADC}+\widehat{BDC}=180^0\\\widehat{AEB}+\widehat{CEB}=180^0\end{matrix}\right.\)
$\widehat {ADC} = \widehat {AEB}$
`->` $\widehat {CEB} = \widehat {BDC}$
Ta có:\(\left\{{}\begin{matrix}\text{AB = AD + DB}\\\text{AC = AE + EC}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{AD = AE}\end{matrix}\right.\)
`-> \text {BD = EC}`
Xét `\Delta BMD` và `\Delta CME`:
\(\widehat{\text{DBM}}=\widehat{\text{ECM}}\left(\text{CMT}\right)\)
\(\text{BD = CE (CMT)}\)
\(\widehat{\text{BDM}}=\widehat{\text{CEM}\text{ }}\text{ }\left(\text{CMT}\right)\)
`=> \Delta BMD = \Delta CME (g-c-g)`
`c,` Đề có phải là "Chứng minh AM là phân giác của góc BAC" ?
Vì `\Delta BMD = \Delta CME (b)`
`-> \text {MB = MC (2 cạnh tương ứng)}`
Xét `\Delta BAM` và `\Delta CAM`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\text {AM chung}`
`\text {MB = MC (CMT)}`
`=> \Delta BAM = \Delta CAM (c-c-c)`
`->` $\widehat {BAM} = \widehat {CAM} (\text {2 góc tương ứng})$
`-> `\(\text{AM là tia phân giác của }\widehat{\text{BAC}}\)
a: Kẻ DH và EK lần lượt vuông góc với BC
=>DH//EK
H,B lần lượt là hình chiếu của D,B trên BC
=>HB là hình chiếu của DB trên BC
K,C lần lượt là hình chiếu của E,C trên BC
=>KC là hình chiếu của EC trên BC
Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
DB=EC
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=KC và DH=EK
b: Xét ΔABE và ΔACD có
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
c: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
d: Xét ΔABM và ΔACM có
AM chung
MB=MC
AB=AC
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
a, Xét tam giác ABE và tam giác ACD
AB = AC
AE = AD
^A _ chung
Vậy tam giác ABE = tam giác ACD (c.g.c)
=> BE = CD ( 2 cạnh tương ứng )
=> ^ABE = ^ACD ( 2 góc tương ứng )
b, Ta có BD = AB - AD ; EC = AC - AE => BD = EC
Xét tam giác KBD và tam giác KCE có
^BKD = ^CKE ( đối đỉnh )
^KBD = ^KCE (cmt)
BD = CE (cmt)
Vậy tam giác KBD = tam giác KCE (g.c.g)
c, Xét tam giác ABH và tam giác ACH có
^B = ^C
AH _ chung
AB = AC
Vậy tam giác ABH = tam giác ACH ( c.g.c )
=> ^BAH = ^CAH ( 2 góc tương ứng )
=> AH là đường phân giác
hay AK là đường phân giác
d, Xét tam giác ABC cân tại A có AK là phân giác đồng thời là đường cao
hay AK vuông BC
e, Ta có AD/AB = AE/AC => DE//BC (Ta lét đảo)
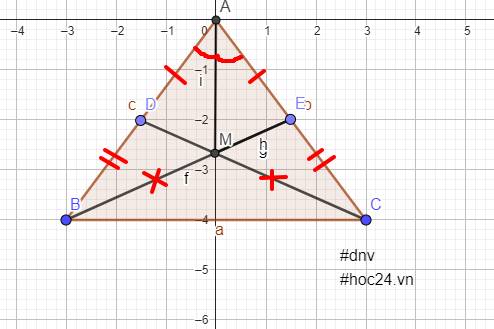
CM: a) Do t/giác ABC cân tại A => AB = AC và góc B = góc C
Ta có : AD + DB = AB
AE + EC = AC
và AD = AE(gt); AB = AC(cmt)
=> DB = CE
Xet t/giác BDC và t/giác CEB
có DB = CE (cmt)
góc B = góc C (cmt)
BC : chung
=> t/giác BDC = t/giác CEB (c.g.c)
=> BE = DC (hai cạnh tương ứng)
b) Ta có: t/giác BDC = t/giác CEB (cmt)
=> góc BDC = góc BEC (hai góc tương ứng)
=> góc EBC = góc DCB (hai góc tương ứng)
Mà góc ABE + góc EBC = góc B
góc ACD + góc DCB= góc C
và góc B = góc C (cmt)
=> góc EBA = góc DCA
Xét t/giác BMD và t/giác CME
có góc BDM = góc CEM (cmt)
DB = EC (Cmt)
góc DBM = góc MCE(cmt)
=> t/giác BMD = t/giác CME(g.c.g)
c) Ta có: t/giác BMD = t/giác CME (cmt)
=> BM = CM (hai cạnh tương ứng)
Xét t/giác ABM và t/giác ACM
có AB = AC (cmt)
BM = CM (cmt)
AM : chung
=> t/giác ABM = t/giác ACM (c.c.c)
=> góc BAM = góc CAM (hai góc tương ứng)
=> AM là tia p/giác của góc BAC
CM
a) Vì \(\Delta ABC\)cân tại A \(\Rightarrow\hept{\begin{cases}\widehat{ABC}=\widehat{ACB}\left(tinhchat\right)\\AB=AC\left(dinhnghia\right)\end{cases}}\)
Ta có:\(\hept{\begin{cases}AB=AC\\AD=AE\\AD+DB=AB;AE+EC=AC\end{cases}}\)\(\Rightarrow DB=EC\)
Xét \(\Delta BDC\)và \(\Delta CEB\)có:
\(\hept{\begin{cases}DB=EC\left(cmt\right)\\\widehat{ABC}=\widehat{ACB\left(cmt\right)}\\BCchung\end{cases}}\)\(\Rightarrow\)\(\Delta BDC\)=\(\Delta CEB\) (c-g-c)
\(\hept{\begin{cases}BE=CD\left(2canhtuongung\right)\\\widehat{BDC}=\widehat{BEC}\left(2canhtuongung\right)\\\widehat{B1}=\widehat{C1}\left(2goctuongung\right)\end{cases}}\)
b) Xét \(\Delta MBC\)có \(\widehat{B1}=\widehat{C1}\left(cmt\right)\)
\(\Rightarrow\Delta MBC\)cân tại A
\(\Rightarrow MB=MC\left(tinhchat\right)\)
Ta có: \(\hept{\begin{cases}BE=CD\left(cmt\right)\\MB=MC\left(cmt\right)\\DM+MC=DC;ME+MB=EB\end{cases}}\)\(\Rightarrow DM=ME\)
Xét \(\Delta BMD\)và \(\Delta CME\)có:
\(\hept{\begin{cases}\widehat{M1}=\widehat{M2}\left(2gocdoidinh\right)\\MD=ME\left(cmt\right)\\\widehat{BDC}=\widehat{BEC}\left(cmt\right)\end{cases}}\)\(\Rightarrow\Delta BMD=\Delta CME\)( g-c-g)
c) Bạn làm phần a và b trước nhé mình nghĩ phần c rồi nói