Biết ( Xo; Yo; Zo) là nghiệm nguyên dương của phương trình X^2+Y^2+Z^2=XY+3Y+2Z-4 .Tính Xo+Yo+Zo
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 11 2018
34cm=0,34m ; 36cm=0,35m ; 44cm=0,44m
500g=0,5kg
khi cố định một đầu của lò xo đầu còn lại treo vật
\(F_{đh}=P\)
khi treo m1 \(F_{đh1}=P_1\Rightarrow k.\left(l_1-l_0\right)=m_1.g\) (1)
khi treo m2 \(F_{đh2}=P_2\Rightarrow k.\left(l_2-l_0\right)=m_2.g\) (2)
lấy (1) chia cho (20
\(\Rightarrow\dfrac{l_1-l_0}{l_2-l_0}=\dfrac{m_1}{m_2}\)\(\Rightarrow m_2=\)0,05kg
\(\Rightarrow k=5\)0N/m
VT
20 tháng 12 2019
Ta có F l x = k(l – l 0 ) = P
⇒ k = P 1 /( l 1 - l 0 ) = 5/17 ≈ 294(N/m)
Do độ cứng của lò xo không đổi nên ta có
VT
4 tháng 1 2018
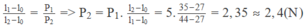
Lời giải
Ta có: W t = 1 2 k Δ l 2 = 1 2 100 0 , 05 2 = 0 , 125 J .
Đáp án: D
20 tháng 2 2023
Cứ vật nặng 20g thì lò xo dãn thêm 0,5cm.
\(\Rightarrow\)Vật nặng 100g thfi lò xo dãn thêm một đoạn \(\Delta l'=\dfrac{100\cdot0,5}{20}=2,5cm\)
Chiều dài tự nhiên của lò xo à:
\(l_0=l-\Delta l'=15-2,5=12,5cm\)
TK
15 tháng 12 2021
Đổi 500 g= 0,5 kg; 25 cm =0,25 m
\(\left|\Delta l\right|=\dfrac{m\cdot g}{k}=\dfrac{0,5\cdot10}{100}=0,05\left(m\right)\)
\(l_0=l'-\left|\Delta l\right|=0,25-0,05=0,2\left(m\right)=20\left(cm\right)\)
VT
13 tháng 11 2019
Khi treo vật có trọng lượng P2, tại vị trí cân bằng, lò xo dãn Δl2 = 80 mm = 0,08 cm , ta có:
P2 = Fđh = k.Δl2 = 200.0,08 = 16(N)
7 tháng 2 2022
Nếu treo quả nặng 200g thì độ dãn lò xo là:
\(\Delta l_1=l_1-l_0=15-12=3cm=0,03m\)
Độ cứng lò xo là:
\(k=\dfrac{F_1}{\Delta l_1}=\dfrac{10m_1}{\Delta l_1}=\dfrac{10\cdot0,2}{0,03}=\dfrac{200}{3}\)N/m
Khi treo quả nặng 400g thì độ dãn lò xo lúc này là:
\(\Delta l_2=\dfrac{F_2}{k}=\dfrac{10m_2}{k}=\dfrac{10\cdot0,4}{\dfrac{200}{3}}=0,06m=6cm\)
Độ dài lò xo khi treo quả nặng 400g là:
\(l_2=\Delta l_2+l_0=6+12=18cm\)
7 tháng 2 2022
đề yêu cầu tìm độ dài lò xo chứ không tìm độ cứng của lò xo nên bạn làm sai yêu cầu rồi
Mình xin phép xóa câu trả lời này
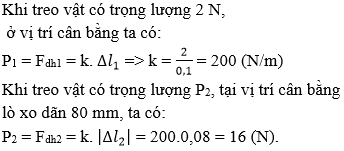
\(x^2+y^2+z^2=xy+3y+2z-4\)
\(\Leftrightarrow4x^2+4y^2+4z^2=4xy+12y+8z-16\)
\(\Leftrightarrow4x^2+4y^2+4z^2-4xy-12y-8z+16=0\)
\(\Leftrightarrow\left(4x^2-4xy+y^2\right)+\left(3y^2-12y+12\right)+\left(4z^2-8z+4\right)=0\)
\(\Leftrightarrow\left(2x-y\right)^2+3\left(y-2\right)^2+4\left(z-1\right)^2=0\)
Xảy ra khi \(\left\{{}\begin{matrix}2x-y=0\\y-2=0\\z-1=0\end{matrix}\right.\)\(\left\{{}\begin{matrix}x=z=1\\y=2\end{matrix}\right.\)
Suy ra \(\left\{{}\begin{matrix}x_0=z_0=1\\y_0=2\end{matrix}\right.\)\(\Rightarrow x_0+y_0+z_0=1+1+2=4\)