Cho tứ diện S.ABC có các cạnh SA, SB; SC đôi một vuông góc và SA=SB=SC=1. Tính cos α, trong đó α là góc giữa hai mặt phẳng (SBC) và (ABC)?
A. cos α = 1 2
B. cos α = 1 2 3
C. cos α = 1 3 2
D. cos α = 1 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D
Ta có V A . M N P = V S . M N P (do M là trung điểm của SA ,
nên d (A, MNP) = d (S ,MNP) . Mà
V S . M N P V S . A B C = S M S A . S N S B . S P S C = 1 8 ⇒ V S . M N P = 1 8 V S . A B C = 2

Đáp án là D
![]()
(do M là trung điểm của SA , nên d (A, MNP) = d (S ,MNP) . Mà
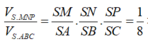
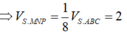

Đáp án B
Gọi M,N lần lượt là trung điểm SC, AB
Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .
Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)
