Cho đường tròn (O). Qua điểm M nằm ngoài đường tròn kẻ 2 tiếp tuyến MA và MB đến đường tròn (A, B là 2 tiếp điểm). Đường thẳng OM cắt AB tại H. Biết rằng OM = 10 cm; R = 5 cm. Tìm khẳng định đúng?
A. OH ⊥ AB
B. A O H ^ = 30 0
C. A O B ^ = 60 0
D. Tất cả đúng




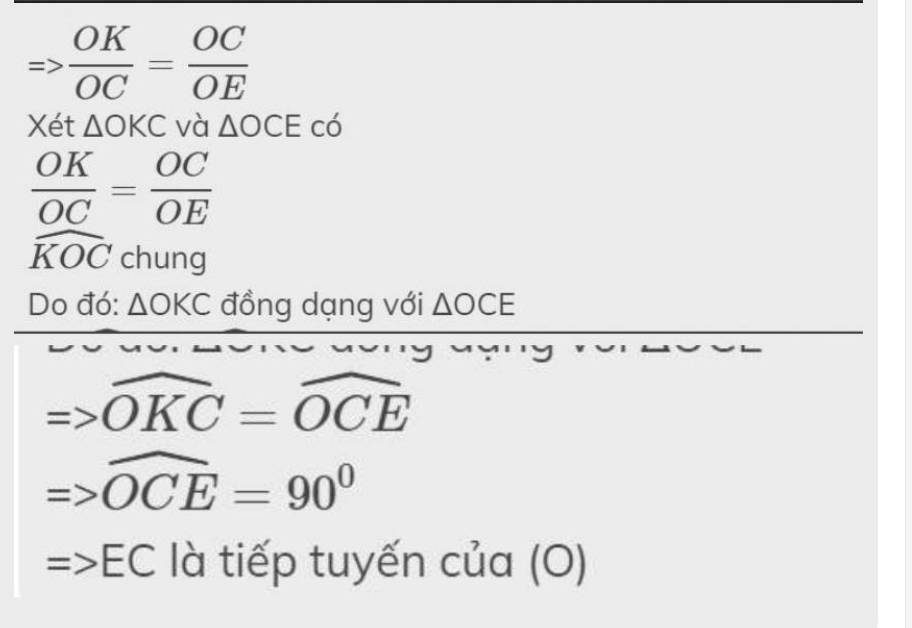



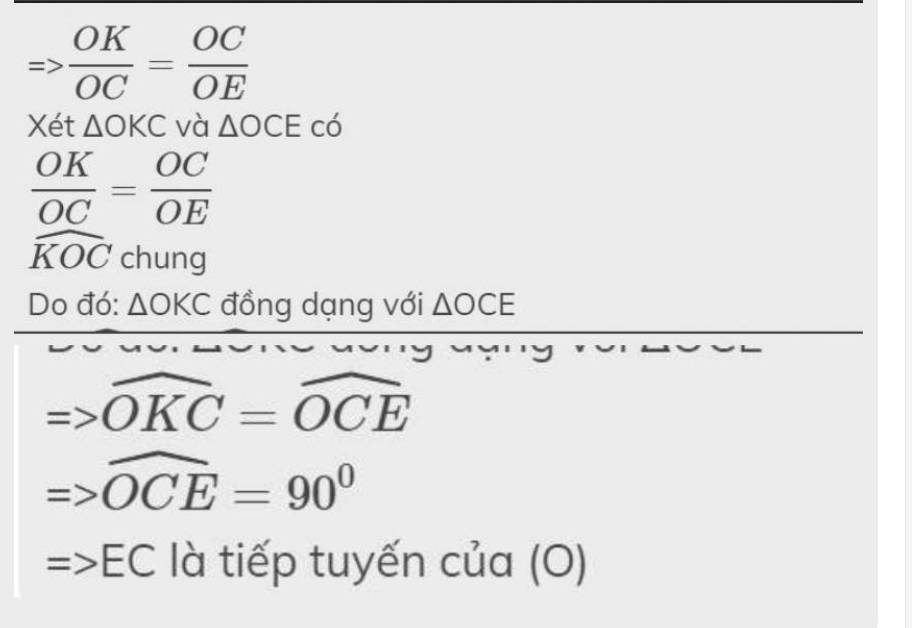


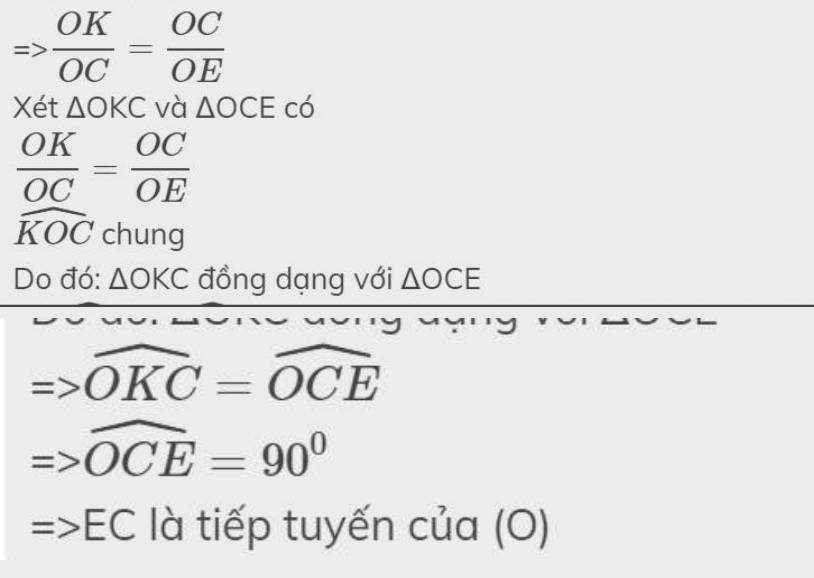



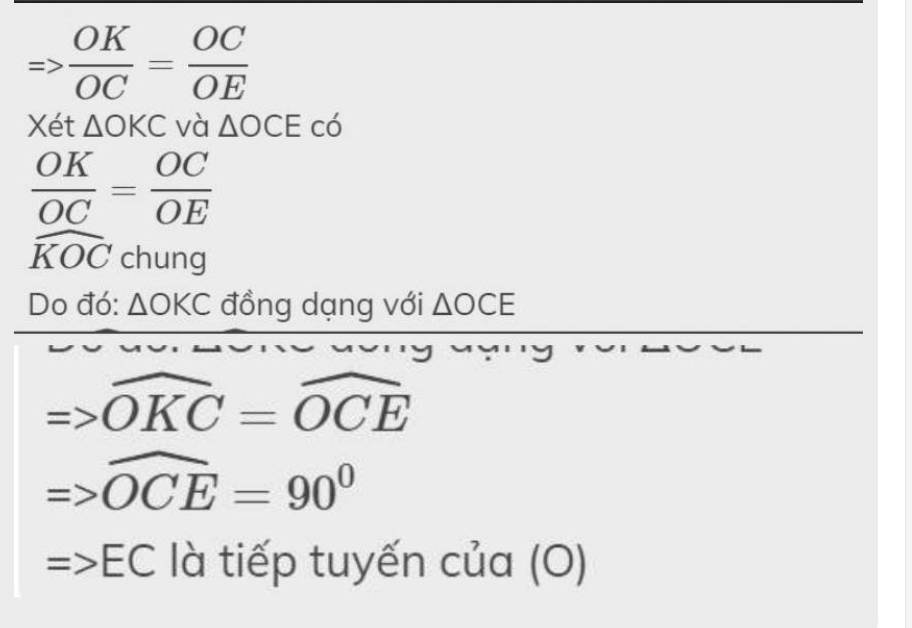



Đáp án A
Ta có: OA = OB = R nên tam giác ABO là cân tại O (1)
Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là tia phân giác của góc AOB (2)
Từ (1) và (2) suy ra: OH là đường cao trong tam giác AOB hay OH ⊥ Ab.
* Xét tam giác vuông AOM có :