Từ một điểm A nằm ngoài (O;R) vẽ hai tiếp tuyến AB và AC.
a) Chứng minh ABOC nội tiếp
b) Vẽ cát tuyến ADE, chứng minh : AD.AE=AB^2
c) Gọi I là trung điểm DE, chứng minh : A;B;O;I;C nằm trên 1 đường tròn
h) Chứng minh IA là phân giác của góc BIC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1
Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O
Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE
Hay OA là trung trực của BE
\(\Rightarrow AB=AE\)
Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)
\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)
11 tháng 1 2022
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
c: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
Xét ΔBAD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(1\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)
hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
\(\widehat{HAE}\) chung
Do đó: ΔAEH\(\sim\)ΔAOD
Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)
CM
1 tháng 3 2018
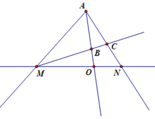
Tia MB cắt đoạn thẳng AO tại điểm B nằm giữa A và O nên tia MB nằm giữa hai tia MA, MO (hay tia MB nằm giữa hai tia MA, MN).
Vì tia MB nằm giữa hai tia MA, MN nên tia MB cắt đoạn thẳng AN tại điểm C nằm giữa hai điểm A, N.
Vậy tia MB cắt tia AN tại điểm C nằm giữa A, N.
21 tháng 12 2021
a: Xét tứ giác OMAN có
\(\widehat{OMA}+\widehat{ONA}=180^0\)
Do đó: OMAN là tứ giác nội tiếp
21 tháng 1
a: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{IBC}\) là góc tạo bởi tiếp tuyến BI và dây cung BC
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{IBC}=\widehat{BAC}\)
Xét ΔIBC và ΔIAB có
\(\widehat{IBC}=\widehat{IAB}\)
\(\widehat{BIC}\) chung
Do đó: ΔIBC~ΔIAB
=>\(\dfrac{IB}{IA}=\dfrac{IC}{IB}\)
=>\(IB^2=IA\cdot IC\)
c: Xét (O) có
\(\widehat{MBC}\) là góc tạo bởi tiếp tuyến BM và dây cung BC
\(\widehat{CDB}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{MBC}=\widehat{CDB}\)
Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC~ΔMDB
=>\(\dfrac{MB}{MD}=\dfrac{MC}{MB}\)
=>\(MB^2=MD\cdot MC\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1
a. Em tự giải
b.
Ta có: IB là tiếp tuyến (O) tại B nên \(\widehat{BAC}=\widehat{CBI}\) (góc nội tiếp và góc tạo bởi tiếp tuyến - dây cung cùng chắn BC)
Xét hai tam giác ABI và BCI có:
\(\left\{{}\begin{matrix}\widehat{BAC}=\widehat{CBI}\left(cmt\right)\\\widehat{BIA}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta ABI\sim\Delta BCI\left(g.g\right)\)
\(\Rightarrow\dfrac{IA}{IB}=\dfrac{IB}{IC}\Rightarrow IB^2=IC.IA\)
c.
Ta có \(\widehat{BDC}\) và \(\widehat{MBC}\) là góc nội tiếp và góc tạo bởi tiếp tuyến sây cung cùng chắn BC
\(\Rightarrow\widehat{BDC}=\widehat{MBC}\)
Xét hai tam giác MBD và MCB có:
\(\left\{{}\begin{matrix}\widehat{BMD}\text{ chung}\\\widehat{BDC}=\widehat{MBC}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta MBD\sim\Delta MCB\left(g.g\right)\)
\(\Rightarrow\dfrac{MB}{MC}=\dfrac{MD}{MB}\Rightarrow MB^2=MC.MD\)
Đẳng thức cuối em ghi sai.
Do I là trung điểm MB \(\Rightarrow MB=2IB\Rightarrow MB^2=4IB^2\)
\(\Rightarrow MC.MD=4IC.IA\) (đây mới là đẳng thức đúng)