Cho M nằm ngoài(O;R), vẽ các tiếp tuyến MA,MB với (O;R). Vẽ đường kính AC, tiếp tuyến tại C của đường tròn (O;R) cắt AB ở D. Chứng minh:a) Tứ giác MAOB nội tiếp b) AB.AD = 4R^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 11 2023
Gọi H,K lần lượt là các tiếp điểm của các tiếp tuyến cắt nhau tại M của (O;r)
=>OH=OK và OH\(\perp\)MB tại H và OK\(\perp\)MD tại K
Xét (O,R) có
OH,OK lần lượt là khoảng cách từ O xuống các dây AB,CD
OH=OK
Do đó: \(sđ\stackrel\frown{AB}=sđ\stackrel\frown{CD}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2023
Xét hai tam giác IMC và DMI có:
\(\left\{{}\begin{matrix}\widehat{IDM}\text{ chung}\\\widehat{CIM}=\widehat{IDM}\left(\text{góc nội tiếp và góc tiếp tuyến cùng chắn cung IM}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IMC\sim\Delta DMI\) (g.g)
\(\Rightarrow\dfrac{MI}{DM}=\dfrac{MC}{MI}\Rightarrow MI^2=MC.MD\) (đpcm)
CM
30 tháng 5 2017
Đáp án C
Xét tam giác AOB có AO = OB = R nên tam giác AOB cân tại O (1)
Theo tính chất hai tiếp tuyến cắt nhau có OM là đường phân giác của góc AOB (2)
Từ (1) và (2) suy ra: OM là đường trung trực của AB.
Ta có điểm N thuộc đường trung trực của AB nên NA = NB
Suy ra, tam giác NAB là tam giác cân tại N
TD
9 tháng 2 2022
Xét (O) có:
CDA và ABC là 2 góc nội tiếp cùng chắn cung AC
=> góc CDA = góc ABC hay góc MDA= gócMBC
Xét tam giác MDA và tam giác MBC có:
góc MDA = góc MBC(cmt)
góc M chung
=> 2 tam giác trên đồng dạng(g.g)
=>\(\dfrac{MD}{MB}=\dfrac{MA}{MC}\)
=>MA.MB=MC.MD
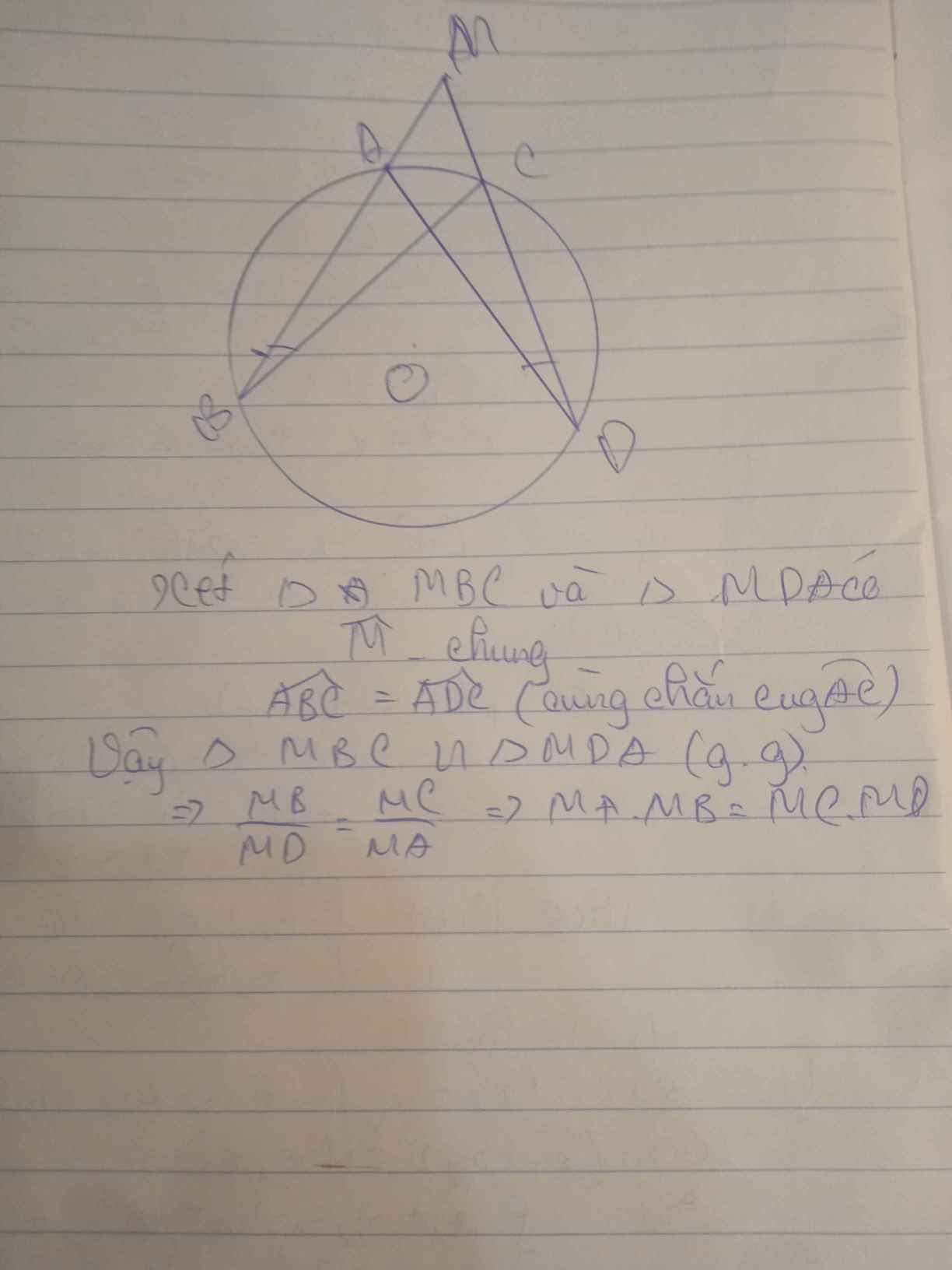
Mình sẽ làm tắt một số chỗ nha vì dễ rồi . Nếu bạn cần đầy đủ thì bảo mình nhé
a) \(\widehat{MAO}=\widehat{MBO}=90^0\)
\(\Rightarrow MAOB\)nội tiép
b) Xét tam giác ABC và tam giác ACD có:
\(\hept{\begin{cases}\widehat{DAC}chung\\\widehat{ABC}=\widehat{ACD}=90^0\end{cases}\Rightarrow\Delta ABC~\Delta ACD\left(g-g\right)}\)
\(\Rightarrow\frac{AC}{AD}=\frac{AB}{AC}\)
\(\Rightarrow AB.AD=AC^2=4R^2\)( đpcm)