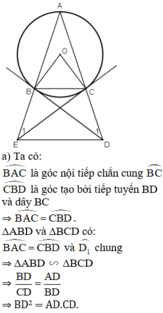
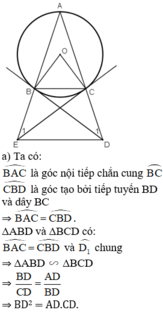
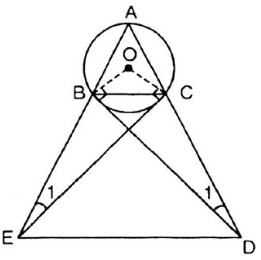
Cho tam giác ABC cân tại A, có cạnh đáy nhỏ hơn cạnh bên nội tiếp trong (O;R). Tiếp tuyến tại B và C cắt nhau tại D.
- C/M: Tứ giác OBDC nội tiếp
- Đường thẳng BD cắt AC tại E. C/m: EB2 = EC . EA
- Tìm M trên cung nhỏ BC vẽ MT vuông góc với BC ( I thuộc BC ). Vẽ MH vuông góc với AB ( H thuộc AB ). Vẽ MF vuông góc với AC (F thuộc AC)
C/m: H,I,F thẳng hàng.
[ giúp mình với ạ ]

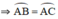
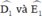 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: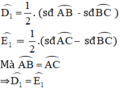

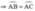
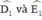 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: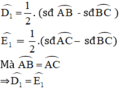



3. C/m: H,I,F thẳng hàng: Tứ giác HBMI nội tiếp ( vì I ,H cùng nhìn BM dưới 1 góc ngoài )
=>Góc HIB = góc HMB (1)
Tứ giác MICF nội tiếp ( góc I + góc F = 1800 )
=> Góc CIF = góc CMF (2)
Tứ giác ABMC nt ( O )
=> góc BAC + góc BMC = 1800
=> góc BAC + góc BMH + góc HMC = 1800 (3)
Tứ giác AHMF nội tiếp ( góc H + góc F = 1800 )
=> Góc HAC + góc HMF = 1800
=> Góc HAC + góc HMC + CMF = 1800 (4)
Từ (3), (4) => Góc BMH = Góc CMF (5)
Từ (1),(2),(5) => Góc HIB = góc FIC
Mà góc BIH + góc HIC = 1800 ( vì IB và IC là 2 tia đối )
=> Góc FIC + góc HIC = 1800nn=> IH và IF là 2 tia đối
=> H,I,F thẳng hàng
các bạn giải cho mình câu 3 thôi câu 1 , 2 mình biết làm rồi ạ