Trên ( O;R), vẽ đường kính AB. lấy C thuộc (O) sao cho AC=R và lấy điểm D bất kì trên cung nhỏ BC (D ko trùng với B,C ). Gọi E là giao điểm của AD và BC. Đường thẳng đi qua E vuông góc với đưởng thẳng AB tại H. C/m tứ giác AHEC là tứ giác nội tiếp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì : \(\overrightarrow{MN}=\overrightarrow{OA}\Rightarrow T_{\overrightarrow{OA}}:M\rightarrow N\). Do đó N nằm trên đường tròn ảnh của (O;R) . Mặt khác N lại nằm trên (O’;R’) do đó N là giao của đường tròn ảnh với với (O’;R’) . Từ đó suy ra cách tìm :
- Vè đường tròn tâm A bán kính R , đường tròn náy cắt (O’;R’) tại N
- Kẻ đường thẳng d qua N và song song với OA , suy ra d cắt (O;R) tại M

+) Tam giác AMB nội tiếp đường tròn (O) có AB là đường kính nên là tam giác vuông.
=> \(AM\perp MB\)
N và B đối xứng qua M nên MN = MB
+) Tam giác NAB có AM vừa là đường cao vừa là trung tuyến nên là tam giác cân.
=> AN = AB = không đổi
Vậy khi M di động trên đường tròn (O) thì N di động trên đường tròn (A; AB)
Ta lại có: AO là đường nối tâm, AB là bán kính đường tròn (A), OB là bán kính đường tròn (O).
Mà AO = AB - OB
Vậy đường tròn (O; OB) tiếp xúc đường tròn (A; AB) tại B.

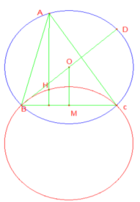
mình sửa lại rồi
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét tứ giác ACEH có
\(\widehat{ACE}+\widehat{AHE}=180^0\)
Do đó: ACEH là tứ giác nội tiếp