Cho lăng trụ tam giác đều A B C . A ' B ' C ' có cạnh đáy bằng 2a; O là trọng tâm tam giác ABC và A ' O = 2 a 6 3 . Tính thể tích V của khối lăng trụ A B C . A ' B ' C ' .
A. V = 4 a 3
B. V = 2 a 3
C. V = 4 a 3 3
D. V = 2 a 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi H là trọng tâm tam giác đều ABC có diện tích S A B C = a 3 2
A 1 cách đều A, B, C
![]()
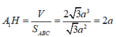
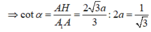
⇒ α = 60 o

Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .


Đáp án B
Ta có: A O = 2 3 2 a 2 − a 2 = 2 a 3 3
A ' A = 2 a 6 3 2 − 2 a 3 3 2 = 2 a 3 S A B C = 1 2 . 2 a 2 sin 60 ∘ = a 2 3
Thể tích khối lăng trụ là: V = S A B C . A ' A = a 2 3 . 2 a 3 = 2 a 3 .