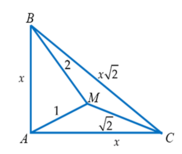
Cho \(\Delta\)ABC cân tại A . Điểm M nằm bên trong tam giác sao cho MA=2cm; MB=3cm và \(\widehat{AMC}\)= 135\(^0\). Tính MC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


trên nửa mặt phẳng bờ AM không chứa điểm B vẽ tam giác ADM vuông cân tại A
Ta có : \(\widehat{DMC}=\widehat{AMC}-\widehat{AMD}=90^o\)
\(\Rightarrow\)\(\Delta ADC=\Delta AMC\left(c.g.c\right)\)
\(\Rightarrow\)DC = MB = 3cm
Xét \(\Delta AMD\)vuông tại A, theo định lí Py-ta-go, ta có :
MD2 = MA2 + AD2 = 22 + 22 = 8
Xét \(\Delta MCD\)vuông tại M , theo định lí Py-ta-go, ta có :
CD2 = MD2 + MC2 \(\Rightarrow\)MC2 = CD2 - MD2 \(\Rightarrow\)MC2 = 32 - 8 = 1 \(\Rightarrow\)MC = 1 cm

trên nửa mặt phẳng bờ AM ko chứa điểm B dựng tam giác ADM zuông cân tại đỉnh A
ta có AD=MA=2cm
\(\widehat{AMD}=45^0;\widehat{DMC}=\widehat{AMC}-\widehat{AMD}=90^0\)
Xét tam giác ADC zà tam giác AMB có
\(\hept{\begin{cases}AD=AM\\AC=Ab\left(gt\right)\\\widehat{DAC}=\widehat{MAB}\end{cases}}\)(cùng phụ zới góc CAM , ( cái này là giải thích tại sao góc DAC= góc MAB nha)
=> 2 tam giác trên = nhau
=>\(DC=MB\)
tam giác AMD zuông tại A nên \(MD^2=MA^2+AD^2\)
=>\(MD^2=2^2+2^2=8\)
tam giác MDC zuông tại M nên
\(DC^2=MD^2+MC^2\Leftrightarrow3^2=8+MC^2=>MC=1\)


Answer:
D C B M A
Trên nửa mặt phẳng bờ AM không chứa B xác định điểm D sao cho tam giác ADM vuông cân tại A
Lúc này AD = AM = 2cm và góc AMD = 45 độ
=> Góc DMC = góc AMC - góc AMD = 135 độ - 45 độ = 90 độ
Ta xét tam giác ADC và tam giác AMB:
AC = AB (gt)
AD = AM
Góc DAC = góc MAB
=> Tam giác ADC = tam giác AMB (c.g.c)
=> BM = CD = 3cm
Ta xét tam giác ADM vuông tại A, áp dụng định lý Pytago:
\(MD^2=MA^2+AD^2=2^2+2^2=8\)
Ta xét tam giác MDC vuông tại M, áp dụng định lý Pytago:
\(CD^2=MD^2+MC^2\Rightarrow3^2=8+MC^2\Rightarrow MC=1cm\)