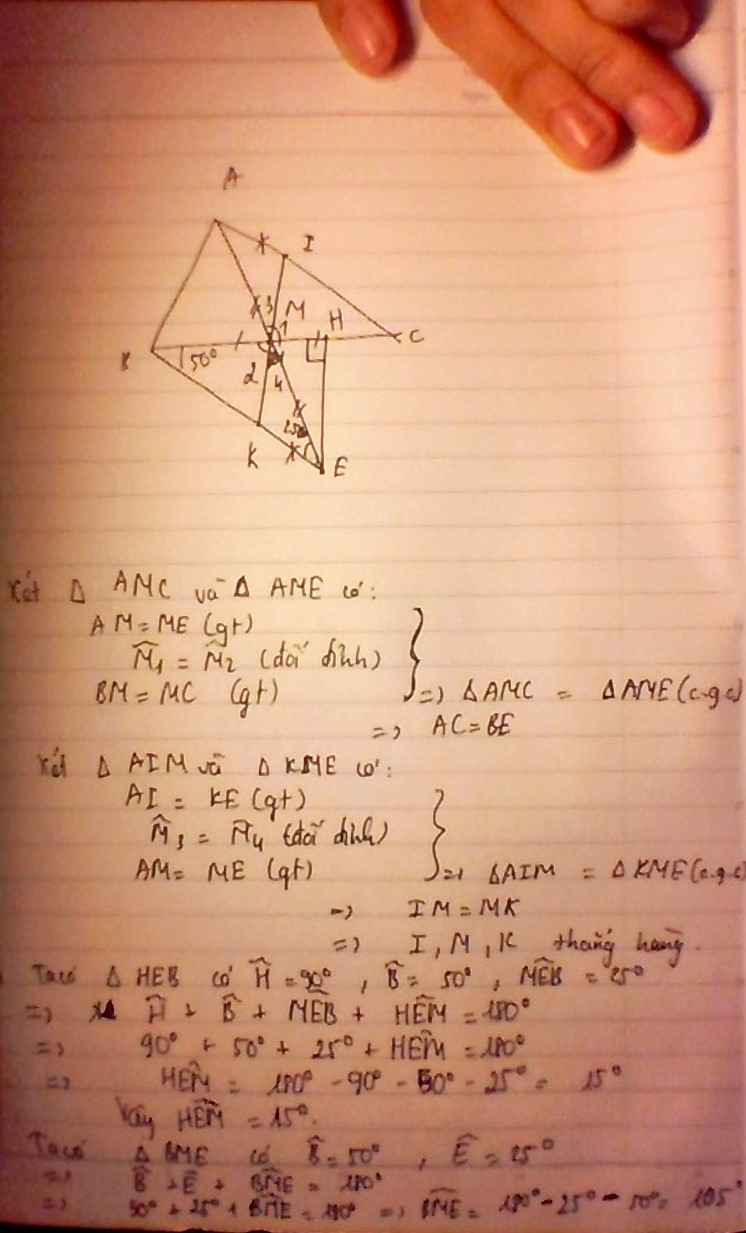Question

[Đoraemon]

1. Cho tam giác ABC, M là trung điểm của BC . Trên tia đối của tia MA lấy điểm E sao choME= MA. Chứng minh rằng: 

a) AC = EB và AC // Be

b) gọi I là một trên AC; K là một điểm trên EB sao choAI= EK. Chứng minh ba điểm I, M, K thẳng hàng

c) Từ E kẻ EH vuông góc BC ( H thuộc BC ) Biết góc HBE= 50 độ; MEB = 25 độ. Tính góc HẺM và BME

2) Cho tam giác ABC có góc B và góc C nhỏ hơn 90 độ. Vẽ ra phía ngoài tam giác ấy các tam giác cân ABD và ACE( trong đó góc ABD và góc ACE đều bằng 90 độ) vẽ DI và EK cùng vuông góc với đường thẳng BC . Chứng minh rằng:

a) BI = CK; EK = HC

b)BC=DI+ EK

3/ Cho tam giác ABC có góc A > 90 độ. Gọi là trung điểm của cạnh BC . Trên tia đối của tia IB lấy điểm D sao cho IB = ID. Nối C với D

a) Chứng minh tam giác AIB = tam giác CID

b) gọi M là trung điểm của BC , N là trung điểm của CD. Chứng minh rằng I là trung điểm của LN

c) Chứng minh góc AIB<góc BIC

d) Tìm điều kiện của tam giác ABCđể AC vuông góc với CD

Cần lời giải gấp ạ, mơn nhiều