Cho tứ giác ABCD nội tiếp (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD \(\left(H\in AB;K\in AD\right)\).
a/ CM tứ giác AHIK nội tiếp
b/ CM: IA.IC=IB.ID
c/ CMR: tam giác HIK và tam giác BCD đồng dạng
d/ Gọi S là diện tích tam giác ABD, S' là diện tích tam giác HIK. CMR: \(\dfrac{S'}{S}\le\dfrac{HK^2}{4AI^2}\)

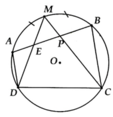

a) Tứ giác AHIK nội tiếp
\(\widehat{AHI}+\widehat{AKI}=90^0+90^0=180^0\)
\(\Rightarrow\text{AHIK nội tiếp}\)
b) \(IA\times IC=IB\times ID\)
\(\text{Xét }\Delta IAB\text{ và }\Delta IDC\text{ có:}\)
\(\widehat{AIB}=\widehat{DIC}\left(\text{2 góc đối đỉnh}\right)\)
\(\widehat{A_1}=\widehat{D_1}\left(\text{cùng chắn }\stackrel\frown{BC}\right)\)
\(\Rightarrow\Delta IAB\sim\Delta IDC\left(g-g\right)\)
\(\Rightarrow\dfrac{IA}{ID}=\dfrac{IB}{IC}\)
\(\Rightarrow IA\times IC=IB\times ID\)
c) \(\Delta HKI\sim\Delta BDC\)
\(\widehat{H_2}=\widehat{A_2}\left(\text{AHIK nội tiếp}\right)\)
\(\widehat{A_2}=\widehat{B_2}\left(\text{cùng chắn }\stackrel\frown{CD}\right)\)
\(\Rightarrow\widehat{H_2}=\widehat{B_2}\) (1)
\(\widehat{K_1}=\widehat{A_1}\left(\text{AHIK nội tiếp}\right)\)
\(\widehat{A_1}=\widehat{D_1}\left(\text{cùng chắn }\stackrel\frown{BC}\right)\)
\(\Rightarrow\widehat{K_1}=\widehat{D_1}\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HKI\sim\Delta BDC\left(g-g\right)\)
d) \(\dfrac{S_{HKI}}{S_{ABD}}\le\dfrac{HK^2}{4AI^2}\)
➤ \(\Delta HKI\sim\Delta BDC\Rightarrow\dfrac{S_{HKI}}{S_{BDC}}=\dfrac{HK^2}{BD^2}\Rightarrow S_{HKI}=\dfrac{HK^2\times S_{BDC}}{BD^2}\)
➤ \(\text{Đặt }T=\dfrac{S_{HKI}}{S_{ABD}}=\dfrac{HK^2\times S_{BDC}}{BD^2\times S_{ABC}}\)
Ta có: \(\dfrac{S_{BDC}}{S_{ABC}}=\dfrac{IC}{IA}\)
\(\Rightarrow T=\dfrac{HK^2\times IC}{BD^2\times IA}=\dfrac{HK^2\times IC}{\left(IB+ID\right)^2\times IA}\)
➤ Áp dụng bất đẳng thức AM - GM
\(\Rightarrow T\le\dfrac{HK^2\times IC}{4\times IB\times ID\times IA}=\dfrac{HK^2\times IC}{4\times IA\times IC\times IA}=\dfrac{HK^2}{4IA^2}\left(đpcm\right)\)