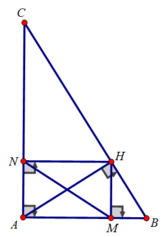
Cho tgABC vuông tại A, đường cao AH. Vẽ HM vg^AB; HN vg^ AC
Biết AH=2cm,BC=5cm.Tính diện tích AMHN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
hay \(\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)

a: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
b: Giả sử AB<AC
Đặt HB=x; HC=y
Theo đề, ta có: x+y=15 và xy=36
=>x=3 và y=12
=>AB=căn 3*15=3căn 5cm; AC=căn 12*15=6*căn 5(cm)
AM=AH^2/AB=6^2/3*căn 5=12/căn 5(cm)
AN=AH^2/AC=6^2/6căn 5=6/căn 5(cm)
S AMHN=AM*AN=72/5cm2

a) Xét tam giác ABC vuông tại A, đường cao AH có:
B C 2 = A B 2 + A C 2 = 25 ⇒ BC = 5(cm)
AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)
BH + CH = BC⇒ CH = BC - BH = 5 - 1,8 = 3,2 (cm)
A H 2 = BH.CH ⇒ AH = B H . C H = 1 , 8 . 3 , 2 = 2,4 (cm)
Xét tứ giác AMHN có:
∠(MAN) = ∠(ANH) = ∠(AMH) = 90 0
⇒ Tứ giác AMHN là hình chữ nhật
⇒ MN = AH = 2,4 (cm)


c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

a: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
b: Sửa đề: \(AE\cdot EB+AF\cdot FC=HB\cdot HC\)
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot EB=HE^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot FC=HF^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(HB\cdot HC=AH^2\)
\(AE\cdot EB+AF\cdot FC=HE^2+HF^2\)
\(=EF^2=AH^2=HB\cdot HC\)

a, Xét tam giác AHM và tam giác ACH ta có :
^H = ^HMA = 900
^A _ chung
Vậy tam giác AHM ~ tam giác ACH ( g.g )
\(\Rightarrow\frac{AH}{AC}=\frac{AM}{AH}\)( tỉ số đồng dạng ) \(\Rightarrow AH^2=AM.AC\)
b, đề sai ko ?
Cho tam giác ABC cân tại A, trung tuyến AM, O là trung điểm của AM. Tia BO cắt AC tại D, CO cắt AB tại E. Cho biết diện tích tam giác ADE=a^2
Tính diện tích tam giác ABC