Cho ABC vuông tại A. Hạ AH vuông BC (H thuộc BC); HM vuông AB, HN vuông AC. a) Chứng minh: AB2 = BH.BC. b) Chứng minh: AMN đồng dạng với ACB. c) Gọi O là trung điểm của BC. Chứng minh: AOvuông MN tại I. d) Cho Pamn= 12 cm, Pabc= 24 cm .Tính ABC^?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NT
1
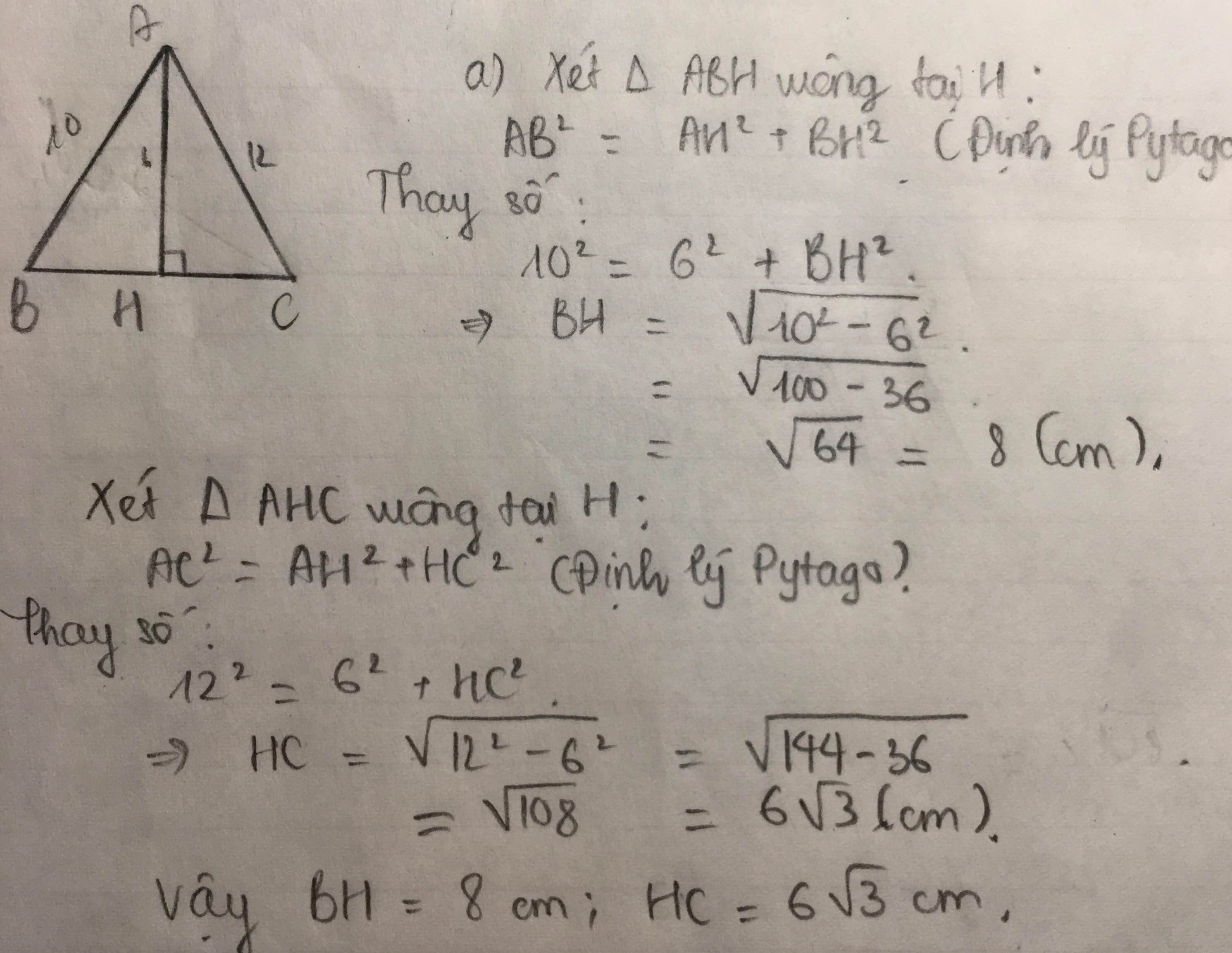
a: Xét ΔABC vuông tại A có AH là đường cao
nên BA^2=BH*BC
b: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
=>ΔAMN đồng dạng với ΔACB
c: góc NAO+góc ANM
=góc OCA+góc AHM
=góc ACB+góc ABC=90 độ
=>MN vuông góc AO