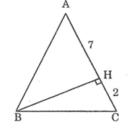
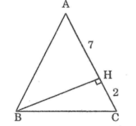
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm



Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên phải: AH = 4cm; HC = 1cm
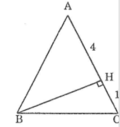

Tam giác ABC cân tại A nên ta có: AB=AC= AH + HC =4+1=5
Trong tam giác vuông BHA ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=52-42=25-16=9
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2
BC2=9+1=10 =>BC=√10

Ta có: AB=AC(ΔABC cân tại A)
nên AB=AH+HC=7+2=9(cm)
Xét ΔAHB vuông tại H có
\(HB^2+HA^2=AB^2\)
\(\Leftrightarrow BH^2=9^2-7^2=81-49=32\)
hay \(HB=4\sqrt{2}\left(cm\right)\)
Xét ΔBHC vuông tại H có
\(BC^2=BH^2+CH^2\)
\(\Leftrightarrow BC^2=\left(4\sqrt{2}\right)^2+2^2=36\)
hay BC=6(cm)

câu a: có 2 bước
bước 1 : tính cạnh BH
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)

Nguyễn Quỳnh Nga làm đc ko mà Spam?
Giải:
Do ABCABC cân nên AB=AC=7+2=9 cm
H là hình chiếu của B lên AC nên BH vuông góc AC
Áp dụng Py - ta - go, ta có:
\(BC=\sqrt{BH^2+2^2}=6\)

hình ạn tư vẽ nha
vì ABC cân nên AB = AC = AH + HC = 9 cm
Xét tam giác ABH : có góc AHB = 90 độ ( vì H là hình chiếu của B trên AC)
Theo định lí Pi-ta-go ta có \(BH^2+AH^2=AB^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2\)
\(\Leftrightarrow BH^2=9^2-7^2\)
\(\Leftrightarrow BH^2=32\Leftrightarrow BH=4\sqrt{2}\)
Xết tam giác BHC vuông tại H theo Định Lí Pi-ta-go ta có
\(BH^2+HC^2=BC^2\)\(\Leftrightarrow\left(4\sqrt{2}\right)^2+2^2=BC^2\)
\(\Leftrightarrow36=BC^2\)\(\Leftrightarrow BC=6cm\)
Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm