Trong hình vẽ có AB vuông góc AD; CD vuông góc AD, CDE= 130 độ và Ê = 130 độ. Chứng minh rằng AB // EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



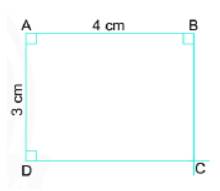
Vẽ đoạn thẳng AB = 4cm.
Sử dụng êke để kẻ đường vuông góc với AB tại A. Trên đường vuông góc này lấy điểm D sao cho đoạn thẳng AD = 3 cm.
Sử dụng êke để kẻ đường vuông góc với AB tại B; kẻ đường vuông góc với AD tại D. Nối hai đường vuông góc này thấy hai đường này cắt nhau tại C.
Ta được, ABCD là hình chữ nhật cần vẽ.

a: Kẻ BH vuông góc CD
Xét tứ giác ABHD có
góc BAD=góc ADH=góc BHD=90 độ
AB=AD
=>ABHD là hình vuông
=>BH=HD=AB=DC/2
=>góc BDH=45 độ
DH=DC/2
=>H là trung điểm của DC
Xét ΔBDC có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBDC cân tại B
=>góc C=45 độ
=>góc ABC=135 độ
c: DC=2*3=6cm
AD=AB=3cm
BC=căn 3^2+3^2=3*căn 2cm
C=6+3+3+3căn 2=12+3căn 2(cm)

a) Ta có:
\(MN \bot CE\) (gt)
\(AB \bot CE\) (gt)
Suy ra \(MN\) // \(AB\)
\(MN\)Mà \(AB\) // \(CD\) (do \(ABCD\) là hình bình hành) nên \(MN\)
// \(CD\)
Xét tứ giác \(MNCD\) ta có:
\(MN\) // \(CD\) (cmt)
\(MD\) // \(CN\) (do \(AD\) // \(BC\))
Suy ra \(MNCD\) là hình bình hành
Lại có:
\(AD = 2AB\) (gt);
\(AD = 2MD\) (do \(M\) là trung điểm của \(AD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(MD = CD\)
Hình bình hành \(MNCD\) có \(MD = CD\) (cmt) nên là hình thoi
b) Vì \(MNCD\) là hình thoi nên \(MD = CD = NC = MN = \frac{1}{2}AD = \frac{1}{2}BC\) (do \(AD = BD\))
Do \(NC = \frac{1}{2}BC\) nên \(N\) là trung điểm của \(BC\)
Xét \(\Delta EBC\) vuông tại \(E\) có \(EN\) là trung tuyến nên \(EN = \frac{1}{2}BC\)
Suy ra \(EN = NB = NC = \frac{1}{2}BC\)
Suy ra \(\Delta NEC\) cân tại \(N\)
Mà \(NF\) là đường cao (do \(MF \bot EC\))
Suy ra \(NF\) cũng là trung tuyến, phân giác, trung trực của \(\Delta NEC\)
Suy ra \(F\) là trung điểm \(EC\)
Xét \(\Delta MEC\) có \(MF\) là đường cao đồng thời là trung tuyến
Suy ra \(\Delta EMC\) cân tại \(M\)
c) Vì \(AB\) // \(MN\) (cmt)
Suy ra \(\widehat {{\rm{AEN}}} = \widehat {{\rm{EMN}}}\) (so le trong)
Mà \(\widehat {{\rm{EMN}}} = \widehat {{\rm{NMC}}}\) (do \(MF\) là phân giác)
\(\widehat {{\rm{NMC}}} = \widehat {{\rm{MCD}}}\) (do \(MN\) // \(CD\))
Suy ra \(\widehat {{\rm{AEM}}} = \widehat {{\rm{MCD}}}\)
Mà \(\widehat {{\rm{MCD}}} = \frac{1}{2}\widehat {{\rm{BCD}}}\) (do \(MNCD\) là hình thoi)
Và \(\widehat {{\rm{BCD}}} = \widehat {{\rm{BAD}}}\) (do \(ABCD\) là hình bình hành)
Suy ra \(\widehat {{\rm{AEM}}} = \frac{1}{2}\widehat {{\rm{BAD}}}\)
Suy ra \(\widehat {BAD} = 2\widehat {AEM}\)


a: AB=DC=8cm
Xét ΔADC vuông tại A có cosD=AD/DC
=>AD=3,38(cm)
b: Xét ΔCAB vuông tại C và ΔHAD vuông tại H có
góc CAB=góc HAD(=góc ACD)
=>ΔCAB đồng dạng với ΔHAD
=>CA/HA=CB/HD
=>CA*HD=CB*HA

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó:ΔABC=ΔADC
b: MK⊥AD
AC⊥AD
Do đó: MK//AC
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
⇒ΔABC=ΔADC
b)
MK⊥AD
AC⊥AD
⇒MK // AC
Bạn cho mình xin hình vẽ nha bạn