Cho hình vuông ABCD. Gọi M,N,P lần lượt là trung điểm của AB;BC;CD.
a)Chứng minh: SMNP = 1/4 SABCD
b)Nếu M;N;P là 1 điểm bất kì trên các cạnh đó. Chứng minh: SMNP < 1/2 SABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2023
Đề sai rồi bạn. E là giao của CM và DN thì E trùng với C rồi bạn
29 tháng 8 2023
Cho hình vuông ABCD. Gọi M , N lần lượt là trung điểm của AB và BC ĐÂY Ạ
CM
23 tháng 7 2019
Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
15 tháng 7 2019
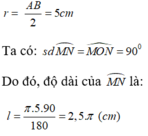
A B C D M N P Q
Bài làm
Vì tứ giác ABCD là hình vuông
=> AB = BC = CD = DA
Mà M; N; P; Q lần lượt là trung điểm của các cạnh AB; BC; CD; DA
=> AM = MB = BN = NC = CP = PD = DQ = QA.
Do đó: MN = NP = PQ = QM.
Xét tứ giác MNPQ có:
MN = NP = PQ = QM
=> Tứ giác MNPQ là hình vuông.
Vậy MNPQ là hình vuông.
# Chúc bạn học tốt #