Cho tam giác ABC(AB=AC)có A=120 .Trung điểm d của AC cắt BC tại D.Trên tia AD lấy điểm E sao cho AE=BD.
a)Tính ABC;ACB;CAD và CM AD = CE
b)CM tam giác DCE là tam giác đều
c)Vẽ trung tuyến AH của tam giác ABC.Tia AH cắt d tại I .CM IC qua trung điểm của DE

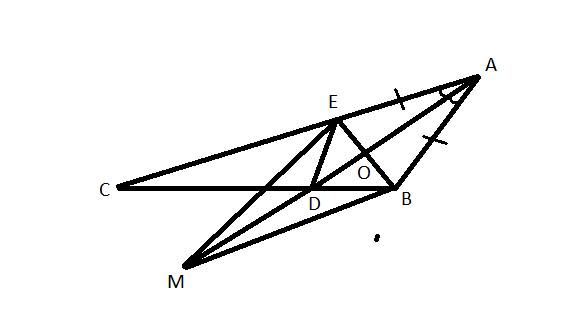
a) Ta có: ΔABC cân tại A(AB=AC)
nên \(\widehat{ABC}=\widehat{ACB}=\frac{180^0-\widehat{A}}{2}\)(số đo của góc ở đáy trong ΔABC cân tại A)
hay \(\widehat{ABC}=\widehat{ACB}=\frac{180^0-120^0}{2}=30^0\)
Gọi F là trung điểm của AC
⇒DF là đường trung trực của AC
hay DF⊥AC
Xét ΔADC có
DF là đường cao ứng với cạnh AC(DF⊥AC)
DF là đường trung tuyến ứng với cạnh AC(do F là trung điểm của AC)
Do đó: ΔADC cân tại D(định nghĩa tam giác cân)
⇒\(\widehat{CAD}=\widehat{ACD}\)(hai góc ở đáy)
mà \(\widehat{ACD}=30^0\)(cmt)
nên \(\widehat{CAD}=30^0\)
Xét ΔABD và ΔACE có
AB=AC(gt)
\(\widehat{DBA}=\widehat{EAC}\left(=30^0\right)\)
BD=AE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
\(\Rightarrow\widehat{ADB}=\widehat{CEA}\)(hai góc tương ứng)
mà \(\widehat{ADB}=\widehat{CDE}\)(hai góc đối đỉnh)
nên \(\widehat{CEA}=\widehat{CDE}\)
Xét ΔCDE có \(\widehat{CED}=\widehat{CDE}\)(\(\widehat{CEA}=\widehat{CDE}\), D∈EA)
nên ΔCDE cân tại C(định lí đảo tam giác cân)
⇒CD=CE
mà AD=CD(ΔADC cân tại D)
nên AD=CE(đpcm)
b) Ta có: ΔADC cân tại D(cmt)
⇒\(\widehat{ADC}=180^0-2\cdot\widehat{CAD}\)(số đo của góc ở đỉnh trong ΔADC cân tại D)
hay \(\widehat{ADC}=180^0-2\cdot30^0=120^0\)
Ta có: \(\widehat{ADC}+\widehat{CDE}=180^0\)(hai góc kề bù)
hay \(\widehat{CDE}=180^0-\widehat{ADC}=180^0-120^0=60^0\)
Xét ΔCDE cân tại C có \(\widehat{CDE}=60^0\)(cmt)
nên ΔCDE đều(dấu hiệu nhận biết tam giác đều)
c) Ta có: AH là đường trung tuyến ứng với cạnh đáy BC của ΔABC cân tại A)
nên AH cũng là đường cao ứng với cạnh BC(định lí tam giác cân)
⇒AH⊥BC
Ta có: \(\widehat{IDH}=\widehat{FDC}\)(hai góc đối đỉnh)(1)
Ta có: DF là đường trung tuyến ứng với cạnh đáy AC của ΔADC cân tại D(F là trung điểm của AC)
nên DF cũng là đường phân giác ứng với cạnh AC(định lí tam giác cân)
⇒DF là tia phân giác của \(\widehat{ADC}\)
⇒\(\widehat{ADF}=\widehat{CDF}=\frac{\widehat{ADC}}{2}=\frac{120^0}{2}=60^0\)(2)
Từ (1) và (2) suy ra \(\widehat{IDH}=\widehat{FDC}=60^0\)(3)
Ta có: \(\widehat{ADH}=\widehat{CDE}\)(hai góc đối đỉnh)
mà \(\widehat{CDE}=60^0\)(cmt)
nên \(\widehat{ADH}=60^0\)(4)
Từ (3) và (4) suy ra \(\widehat{IDH}=\widehat{FDC}=\widehat{ADH}=60^0\)
Xét ΔAIC có
IF là đường trung tuyến ứng với cạnh AC(do F là trung điểm của AC)
IF là đường cao ứng với cạnh AC(DF⊥AC,I∈DF)
Do đó: ΔAIC cân tại I(định lí tam giác cân)
mà IF là đường cao ứng với cạnh đáy AC(DF⊥AC,I∈DF)
nên IF cũng là đường phân giác ứng với cạnh đáy AC(định lí tam giác cân)
⇒IF là tia phân giác của \(\widehat{AIC}\)
⇒\(\widehat{AIC}=2\cdot\widehat{AIF}\)(5)
Ta có: ΔHDI vuông tại H(IH⊥DH)
nên \(\widehat{HDI}+\widehat{HID}=90^0\)(hai góc phụ nhau)
hay \(\widehat{HID}=90^0-60^0=30^0\)
⇒\(\widehat{AIF}=30^0\)(6)
Từ (5) và (6) suy ra
\(\widehat{AIC}=2\cdot30^0=60^0\)
Xét ΔAIC cân tại I có \(\widehat{AIC}=60^0\)(cmt)
nên ΔAIC đều(dấu hiệu nhận biết tam giác đều)
Ta có: \(\widehat{CAD}=30^0\)(cmt)
mà \(\widehat{CAI}=60^0\)(ΔAIC đều)
và tia AD nằm giữa hai tia AC,AI
nên AD là tia phân giác của \(\widehat{CAI}\)
Xét ΔAIC đều có AD là đường phân giác ứng với cạnh IC(do AD là tia phân giác của \(\widehat{CAI}\))
nên AD cũng là đường cao của IC(định lí tam giác cân)
⇒AD⊥IC
hay DE⊥IC
Ta có: ΔCDE đều(cmt)
mà CI là đường cao ứng với cạnh DE(DE⊥IC)
nên CI cũng là đường trung tuyến ứng với cạnh DE
⇒CI đi qua trung điểm của DE(đpcm)
Trung trực d của AC chứ bạn