Cho tam giác ABC nội tiếp tâm Ở trên nửa mặt phẳng bờ BC ko chứa A vẽ tia Ax;Bx sao cho góc xBC=góc A . Chứng minh rằng Bx là tia tiếp tuyến của O
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


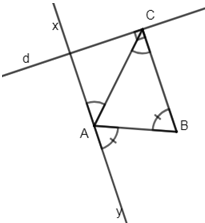
a) Ta có: ˆCAx=ˆACB(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên
suy ra Ax//BC��//�� (1)
ˆBAy=ˆABC(gt)���^=���^(��) mà hai góc đó là hai góc so le trong nên suy ra Ay//BC��//�� (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
⇒⇒ Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà Ax//BC��//�� và Ay//BC��//��
nên suy ra xy//BC��//��
Mà BC⊥d��⊥� nên suy ra d⊥xy

Xét \(\Delta EAC\) và \(\Delta BAD\) có :
AD = AC ( gt )
\(\widehat{CAE}=\widehat{DAB}\)( hai góc đối đỉnh )
AE = AB ( gt )
nên \(\Delta EAC=\Delta BAD\left(c.g.c\right)\)
=> BD = CE ( hai cạnh tương ứng )