Bài 4. Cho tam giác ABC có AB < AC và phân giác AD (D ∈ BC). Trên AC lấy điểm E sao cho
AE = AB. Trên tia AB lấy điểm F sao cho AC = AF. Chứng minh:
a) DB=DE;BF=CE
b) Ba điểm F ,D ,E thẳng hàng
c) BE// FC; AD⊥FC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chắc đề đây này:
Bài 4. Cho tam giác ABC có AB < AC và phân giác AD (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AC = AF. Chứng minh:
a) DB = DE ; BF = CE
b) Ba điểm F , D , E thẳng hàng
c) BE // FC ; AD \(\perp\) FC

a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>BD=ED
b: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
c: Xét ΔDBF và ΔDEC có
DB=DE
góc DBF=góc DEC
BF=EC
=>ΔDBF=ΔDEC
d: AF=AC
DF=DC
=>AD là trung trực của CF
=>AD vuông góc CF

a: Xét ΔADF và ΔADC có
AD chung
\(\widehat{FAD}=\widehat{CAD}\)
AF=AC
Do đó: ΔADF=ΔADC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDF}=180^0\)
=>E,D,F thẳng hàng
c: Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC
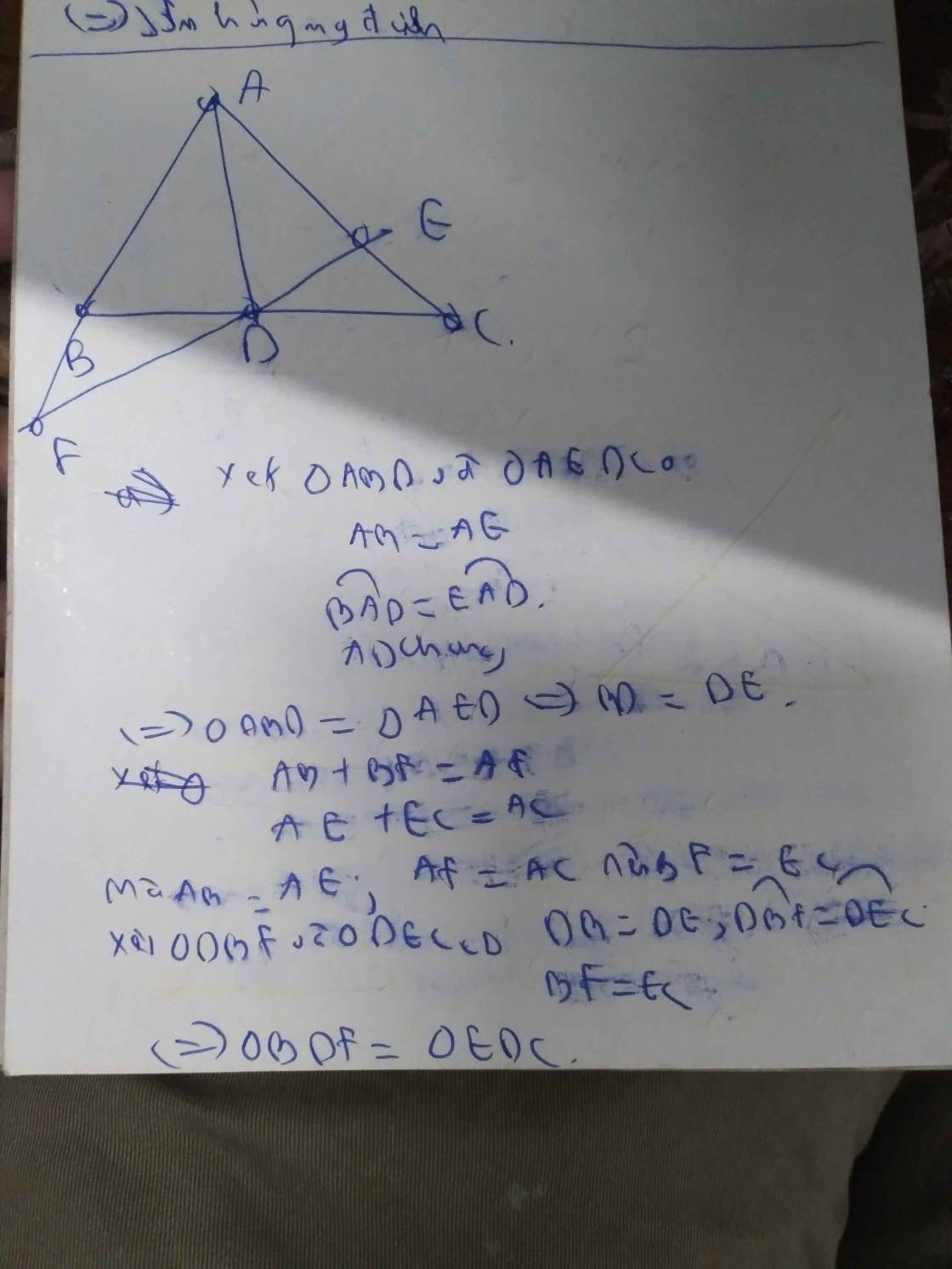
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra DB=DE
Ta có: AB+BF=AF
AE+EC=AC
mà AF=AC
và AB=AE
nên BF=EC
b: Xét ΔBDF và ΔEDC có
BF=EC
\(\widehat{DBF}=\widehat{DEC}\)
BD=DE
Do đó: ΔBDF=ΔEDC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
=>E,D,F thẳng hàng
c: Xét ΔAFC có
AB/AF=AE/AC
nên BE//FC
Ta có: ΔACF cân tại A
mà AD là đường phân giác
nên AD là đường cao