Cho tam giác ABC. Các tia phân giác của góc B và góc C cắt nhau tại O. Kẻ OE; OF; OG theo thứ tự vuông góc với các cạnh AC; AB; BC.a) Chứng minh OE = OF = OG.b) Tia AO cắt cạnh BC tại D. Chứng minh rằng góc BOD bằng góc COG
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 2 2019
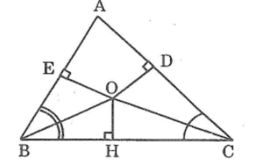
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
∠(OEB) =∠OHB=90o
Cạnh huyền OB chung
∠(EBO) =∠(HBO) ( vì BO là tia phân giác của góc ABC).
Suy ra Δ OEB = Δ OHB (cạnh huyền góc nhọn)
⇒OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
∠(OHC) =∠ODC=90o
Cạnh huyền OC chung
∠(HCO) =∠(DCO)
Suy ra Δ OHC = Δ ODC (cạnh huyền góc nhọn)
⇒OD = OH (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD
22 tháng 11 2016
Ta có hình vẽ:Xét tam giác EOB và tam giác DOC có:
\(\widehat{E}\)=\(\widehat{D}\)=900
\(\widehat{EBO}\)=\(\widehat{DCO}\)
OB = OC
=> tam giác EOB = tam giác DOC
=> OD = OE (2 cạnh tương ứng)
BB
5 tháng 11 2017
Kẻ OK vuông góc vs Bc.
Ta thấy tam giác OKC và ODC
Có:<OKC=<ODC(=90*)
OC:cạnh chung
<OCK=<OCD(do là tia phân giác)
Do đó:Tam giác OKC=tam giác ODC(ch-gn)
=>OK=OD(2 cạnh tương ứng)
C/m tương tự ta được: Tam giác OBE=tam giác OBK(ch-gn)
=>OK =OE(2 cạnh tương ứng)
Mà:OK=OD(c/m trên)
=> OD=OE(đpcm).
1 tháng 2 2022
Xét ΔADO vuông tại D và ΔAEO vuông tại E có
AO chung
\(\widehat{DAO}=\widehat{EAO}\)
Do đó: ΔADO=ΔAEO
Suy ra: OD=OE
19 tháng 8 2016
Kẻ OK vuông góc với BC
Tam giác OKC và ODC là 2 tam giác vuông có:
OC là cạnh chung
góc C1 = góc C2 ( CO là tia phân giác)
=> tam giác OKC = tam giác ODC ( cạnh huyền, góc nhọn)
=> OK = OD ( 2 cạnh tương ứng ) (1)
Chứng minh tương tụ ta cũng có :
tam giác OKB = tam giác OEB (cạnh huyền, góc nhọn)
=> OK = OE ( 2 cạnh tương ứng ) (2)
Từ (1) và (2) => OE = OD
=> Đpcm.