Cho hình chóp S.ABC có SA=SB=SC, tam giác ABC là tam giác vuông tại B, AB=a; BC= a 3 , mặt bên (SBC) tạo với đáy góc 60 0 . Thể tích khối chóp S.ABC là:
A. a 3 6
B. a 3 3
C. 2 a 3 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 1 2019
Đáp án B
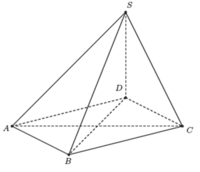
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .
(ABC) . Kẻ AH , AK lần lượt vuông góc với SB , SC tại H và K , có SA = AB = a .
KB
5 tháng 5 2022
1) Ta có : \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
BC \(\perp AB;BC\perp SA\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) \(\Rightarrow\Delta SBC\perp\) tại B
2) \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) . Mà
\(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp HK\) \(\Rightarrow\Delta AHK\perp\) tại H
\(\Delta SAB\perp\) tại A ; \(AH\perp SB\) có : \(AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a^2}{\sqrt{2a^2}}=\dfrac{\sqrt{2}}{2}a\)
AC = \(\sqrt{AB^2+BC^2}=\sqrt{2a^2}=\sqrt{2}a\)
\(\Delta SAC\perp\) tại A có : \(AK\perp SC\) có :
\(AK=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=\dfrac{a.\sqrt{2}a}{\sqrt{a^2+2a^2}}=\dfrac{\sqrt{6}}{3}a\)
\(HK=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{2}{3}a^2-\dfrac{1}{2}a^2}=\dfrac{\sqrt{6}}{6}a\)
\(S_{AHK}=\dfrac{1}{2}HA.HK=\dfrac{1}{2}\dfrac{\sqrt{2}}{2}a.\dfrac{\sqrt{6}}{6}a=\dfrac{\sqrt{3}}{12}a^2\)
3) AH \(\perp\left(SBC\right)\Rightarrow\left(AK;\left(SBC\right)\right)=\widehat{AKH}\)
\(\Delta AHK\perp\) tại H có : \(sin\widehat{AKH}=\dfrac{AH}{AK}=\dfrac{\sqrt{2}}{2}a:\dfrac{\sqrt{6}}{3}a=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{AKH}=60^o\)
CM
26 tháng 1 2019
Đáp án D
Gọi H là trung điểm của BC.
Do tam giác ABC vuông cân tại A nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Mặt khác do SA=SB=SC nên S thuộc trục đường tròn ngoại tiếp ABC
⇒ S H ⊥ A B C A H = B C 2 = a , S H = S A 2 - A H 2 = a A B = A C = B C 2 a 2
Thể tích khối chóp là
V = 1 3 . S H . 1 2 . A B . A C = a 3 3
Chọn D.
Từ giả thiết ta suy ra hình chiếu vuông góc H của S trên (ABC) trùng với tâm đường tròn ngoại tiếp Δ A B C .Mà Δ A B C vuông tại B nên H là trung điểm của AC. Kẻ HK//AB. Ta suy ra, K là trung điểm của BC và ta có góc giữa mặt bên (SBC) tạo với đáy là góc S K H ^ = 60 0 . Ta có H K = a 2 ⇒ S H = a 3 2 và S Δ A B C = a 2 3 2
Vậy V S . A B C = 1 3 S H . S Δ A B C = 1 3 a 3 2 . a 2 3 2 = a 3 4