Cho hình chữ nhật ABCD có AB= 8cm; BC=6cm. VẼ đường cao AH của tam giác ADB.
a)Chứng minh ∆AHB đồng dạng với tam giác BCD.
b. TÍnh S∆AHB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích của hình hộp chữ nhật là
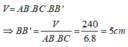
Suy ra: AA’ = BB’ =5cm
Chọn đáp án A

Cho hình chữ nhật ABCD có góc ACB =, BD=8cm. Chu vi hình chữ nhật ABCD là cm.


Chiều rộng là: 24:2-8=4(cm)
EG=AD=4cm
HF=AB=8cm
\(S_{EFGH}=\dfrac{1}{2}\cdot4\cdot8=16\left(cm^2\right)\)
+) AB // CD => góc ABD = BDC (SLT)
Xét tam giác AHB và BCD có : góc AHD = DCB (=90o); góc ABH = BDC
=> tam giác AHB đồng dạng với tam giác BCD ( g- g)
=> AH/BC = AB/BD
+) Áp dụng ĐL Pi ta go trong tam giác ABD có: BD2 = AB2 + AD2 = 82 + 62 = 102 => BD = 10 cm
=> AH/6 = 8/10 => AH = 4,8 cm
+) Áp dụng ĐL Pi ta go trong tam giác ABH có: BH2 = AB2 - AH2 = 82 - 4,82 = 40,96 cm => BH = 6,4 cm
=> S(ABH) = AH.BH : 2 = .....